
下面是空間線面位置關(guān)系中傳遞性的部分相關(guān)命題:
①與兩條平行線中一條平行的平面必與另一條直線平行;
②與兩條平行線中一條垂直的平面 必與另一條直線垂直;
③與兩條垂直直線中一條平行的平面必與另一條直線垂直;
④與兩條垂直直線中一條垂直的平面必與另一條直線平行;
⑤與兩個(gè)平行平面中一個(gè)平行的直線必與另一個(gè)平面平行;
⑥與兩個(gè)平行平面中一個(gè)垂直的直線必與另一個(gè)平面垂直;
⑦與兩個(gè)垂直平面中一個(gè)平行的直線必與另一個(gè)平面垂直;
⑧與兩個(gè)垂直平面中一個(gè)垂直的直線必與另一個(gè)平面平行.
其中正確的命題個(gè)數(shù)有________個(gè).

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
若 是三條互不相同的空間直線,
是三條互不相同的空間直線, 是兩個(gè)不重合的平面,
是兩個(gè)不重合的平面,
則下列命題中為真命題的是 (填所有正確答案的序號(hào)).
①若 則
則 ; ②若
; ②若 則
則 ;
;
③若 則
則 ; ④若
; ④若 則
則
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
已知直線l⊥平面α,直線mÍ平面β,則下列四個(gè)命題:
①若α∥β,則l⊥m; ②若α⊥β,則l∥m;
③若l∥m,則α⊥β; ④若l⊥m,則α∥β.
其中正確命題的序號(hào)是
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在平面幾何里,有勾股定理:“設(shè)△ABC的兩邊AB,AC互相垂直,則AB2+AC2=BC2.”拓展到空間,類比平面幾何的勾股定理,研究三棱錐的面面積與底面面積間的關(guān)系。可以得出的正確結(jié)論是:“設(shè)三棱錐A—BCD的三個(gè)側(cè)面ABC、ACD、ADB兩兩相互垂直,則 ”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
已知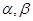 是兩個(gè)互相垂直的平面,
是兩個(gè)互相垂直的平面, 是一對(duì)異面直線,下列五個(gè)結(jié)論:
是一對(duì)異面直線,下列五個(gè)結(jié)論:
(1) ,
, (2)
(2)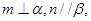 (3)
(3)
(4) (5)
(5) 。其中能得到
。其中能得到 的結(jié)論有 (把所有滿足條件的序號(hào)都填上)
的結(jié)論有 (把所有滿足條件的序號(hào)都填上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
如圖,正方體 的棱長(zhǎng)為1,
的棱長(zhǎng)為1, 為
為 的中點(diǎn),
的中點(diǎn), 為線段
為線段 上的動(dòng)點(diǎn),過點(diǎn)
上的動(dòng)點(diǎn),過點(diǎn) 的平面截該正方體所得的截面記為
的平面截該正方體所得的截面記為 ,則下列命題正確的是 (寫出所有正確命題的編號(hào)).
,則下列命題正確的是 (寫出所有正確命題的編號(hào)).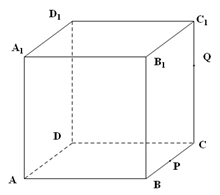
①當(dāng)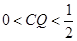 時(shí),
時(shí), 為四邊形
為四邊形
②當(dāng) 時(shí),
時(shí), 為等腰梯形
為等腰梯形
③當(dāng) 時(shí),
時(shí), 與
與 的交點(diǎn)
的交點(diǎn) 滿足
滿足
④當(dāng) 時(shí),
時(shí), 為六邊形
為六邊形
⑤當(dāng) 時(shí),
時(shí), 的面積為
的面積為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
一個(gè)正方體的六個(gè)面上分別標(biāo)有A,B,C,D,E,F,下圖是正方體的兩種不同放置,則與D面相對(duì)的面上的字母是________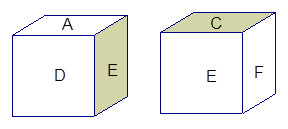
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com