
已知R上的連續函數g(x)滿足:①當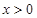 時,
時,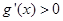 恒成立(
恒成立(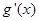 為函數
為函數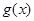 的導函數);②對任意的
的導函數);②對任意的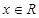 都有
都有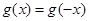 ,又函數
,又函數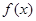 滿足:對任意的
滿足:對任意的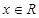 ,都有
,都有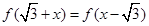 成立。當
成立。當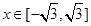 時,
時,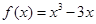 。若關于
。若關于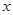 的不等式
的不等式 對
對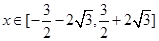 恒成立,則
恒成立,則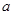 的取值范圍是( )
的取值范圍是( )
A、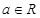 B、
B、
C、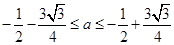 D、
D、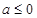 或
或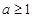
D
【解析】
試題分析:因為函數g(x)滿足:當x>0時,g'(x)>0恒成立,且對任意x∈R都有g(x)=g(-x),所以函數g(x)是R上的偶函數且在[0,+∞)上為單調遞增函數,且有g(|x|)=g(x),所以g|f(x)|≤g(a2-a+2)在R上恒成立,∴|f(x)|≤|a2-a+2|對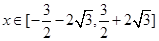 恒成立,
恒成立,
只要使得定義域內|f(x)|max≤|a2-a+2|,由于當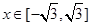 時,
時,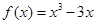 ,
,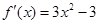
令 =0解得x=-1或x=1,可得函數
=0解得x=-1或x=1,可得函數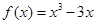 在(
在(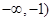 和(1,+
和(1,+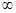 )上是增函數,在(-1,1)上是減函數,f(-1)=2是極大值,f(1)=-2是極小值.
)上是增函數,在(-1,1)上是減函數,f(-1)=2是極大值,f(1)=-2是極小值.
所以函數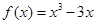 在
在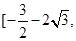 -1]和[1,
-1]和[1,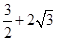 ]上是增函數,在(-1,1)上是減函數,
]上是增函數,在(-1,1)上是減函數,
即f(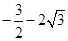 )<f(-1)=2,f(1)>f(
)<f(-1)=2,f(1)>f(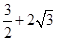 )=f[(
)=f[( ]=f[(
]=f[(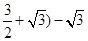 ]=f(
]=f(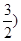 =
=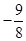 ,
,
所以函數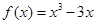 在
在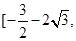 -1]和[1,
-1]和[1, 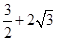 ]上最大值是2.所以2≤|a2-a+2|,解得
]上最大值是2.所以2≤|a2-a+2|,解得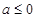 或
或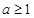 ,故選D.
,故選D.
考點:1.函數的周期性;2.抽象函數及其應用.


 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:高中數學 來源: 題型:
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| A、a≥1或a≤0 | ||||||||||||
| B、0≤a≤1 | ||||||||||||
C、-
| ||||||||||||
| D、a∈R |
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川成都外國語學校高三12月月考理科數學試卷(解析版) 題型:選擇題
已知R上的連續函數g(x)滿足:①當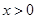 時,
時,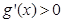 恒成立(
恒成立(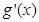 為函數
為函數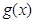 的導函數);②對任意的
的導函數);②對任意的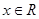 都有
都有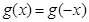 ,又函數
,又函數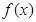 滿足:對任意的
滿足:對任意的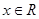 ,都有
,都有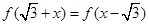 成立。當
成立。當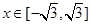 時,
時,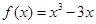 。若關于
。若關于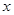 的不等式
的不等式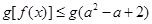 對
對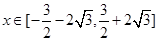 恒成立,則
恒成立,則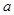 的取值范圍是( )
的取值范圍是( )
A、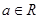 B、
B、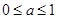
C、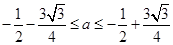 D、
D、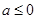 或
或
查看答案和解析>>
科目:高中數學 來源:2010-2011學年遼寧省高三第六次模擬考試數學理卷 題型:選擇題
已知R上的連續函數g(x)滿足:①當x>0時,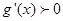 恒成立(
恒成立(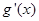 為函數g(x)的導函數);②對任意x∈R都有g(x)=g(-x)。又函數f(x)滿足:對任意的x∈R都有f(
為函數g(x)的導函數);②對任意x∈R都有g(x)=g(-x)。又函數f(x)滿足:對任意的x∈R都有f(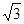 +x)=
+x)=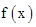 成立,當x∈[
成立,當x∈[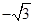 ,
,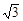 ]時,f(x)=
]時,f(x)=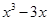 。若關于x的不等式g[f(x)]≤g(
。若關于x的不等式g[f(x)]≤g(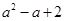 )對 x∈[-
)對 x∈[-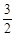 -2
-2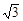 ,
,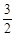 -2
-2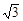 ]恒成立,則a的取值范圍是( )
]恒成立,則a的取值范圍是( )
A.a1或a0 B.0a C.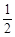
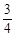
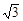 a
a
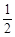 +
+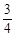
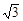 D.aR
D.aR
查看答案和解析>>
科目:高中數學 來源:2011年四川省成都市高考數學一模試卷(理科)(解析版) 題型:選擇題
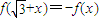 成立,當
成立,當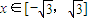 時,f(x)=x3-3x.若關于x的不等式g[f(x)]≤g(a2-a+2)對
時,f(x)=x3-3x.若關于x的不等式g[f(x)]≤g(a2-a+2)對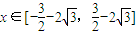 恒成立,則a的取值范圍是( )
恒成立,則a的取值范圍是( )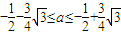 ?
?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com