
如圖所示,已知拋物線E:y2=x與圓M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四個點.
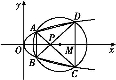
(1)求r的取值范圍;
(2)當四邊形ABCD的面積最大時,求對角線AC、BD的交點P的坐標.
(1)(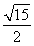 ,4) (2)(
,4) (2)( ,0)
,0)
【解析】
解:(1)將y2=x代入(x-4)2+y2=r2,
并化簡得x2-7x+16-r2=0,①
E與M有四個交點的充要條件是方程①有兩個不等的正根x1,x2,
由此得
解得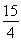 <r2<16.
<r2<16.
又r>0,
所以r的取值范圍是(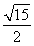 ,4).
,4).
(2)不妨設E與M的四個交點的坐標為:
A(x1, )、B(x1,-
)、B(x1,-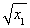 )、C(x2,-
)、C(x2,-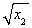 )、D(x2,
)、D(x2,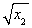 ).
).
則直線AC、BD的方程分別為
y-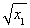 =
= ·(x-x1),
·(x-x1),
y+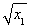 =
=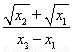 (x-x1),
(x-x1),
解得點P的坐標為(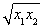 ,0).
,0).
設t=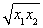 ,
,
由t=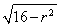 及(1)知0<t<
及(1)知0<t<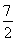 .
.
由于四邊形ABCD為等腰梯形,
因而其面積S=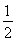 (2
(2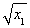 +2
+2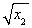 )·|x2-x1|.
)·|x2-x1|.
則S2=(x1+x2+2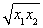 )[(x1+x2)2-4x1x2].
)[(x1+x2)2-4x1x2].
將x1+x2=7,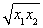 =t代入上式,
=t代入上式,
并令f(t)=S2,
得f(t)=(7+2t)2·(7-2t)(0<t<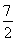 ).
).
求導數,f′(t)=-2(2t+7)(6t-7),
令f′(t)=0得t=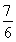 ,t=-
,t=-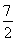 (舍去),
(舍去),
當0<t<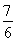 時,f′(t)>0;
時,f′(t)>0;
當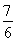 <t<
<t<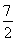 時,f′(t)<0.
時,f′(t)<0.
故當且僅當t=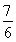 時,f(t)有最大值,
時,f(t)有最大值,
即四邊形ABCD的面積最大.
故所求的點P的坐標為( ,0).
,0).


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
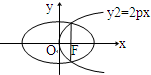
 如圖所示,已知拋物線y2=2px(p>0)的焦點恰好是橢圓
如圖所示,已知拋物線y2=2px(p>0)的焦點恰好是橢圓| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
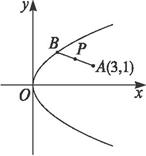
 如圖所示,已知拋物線C1:x2=y,圓M:x2+(y-4)2=1,點P是拋物線C1上一點(異于原點),過點P作圓M的兩條切線,交拋物線C1于A,B兩點,若過M,P兩點的直線l垂直于AB,求直線l的方程.
如圖所示,已知拋物線C1:x2=y,圓M:x2+(y-4)2=1,點P是拋物線C1上一點(異于原點),過點P作圓M的兩條切線,交拋物線C1于A,B兩點,若過M,P兩點的直線l垂直于AB,求直線l的方程.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省無錫市洛社高中高二(上)10月段考數學試卷(解析版) 題型:填空題
 的右焦點F,且兩條曲線的交點連線也過焦點F,則該橢圓的離心率為 .
的右焦點F,且兩條曲線的交點連線也過焦點F,則該橢圓的離心率為 .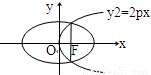
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com