
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,其中
,其中![]() 為參數(shù),
為參數(shù), ![]() ,再以坐標(biāo)原點(diǎn)
,再以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,其中
,其中![]() ,
, ![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn).
兩點(diǎn).
(1)求![]() 的值;
的值;
(2)已知點(diǎn)![]() ,且
,且![]() ,求直線
,求直線![]() 的普通方程.
的普通方程.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)先根據(jù)代入消元法將直線![]() 的參數(shù)方程化為普通方程,利用
的參數(shù)方程化為普通方程,利用![]() 將曲線
將曲線![]() 的極坐標(biāo)方程化為直角坐標(biāo)方程,聯(lián)立直線方程與拋物線方程,利用韋達(dá)定理代入
的極坐標(biāo)方程化為直角坐標(biāo)方程,聯(lián)立直線方程與拋物線方程,利用韋達(dá)定理代入![]() 可得
可得![]() 的值;(2)由直線參數(shù)方程幾何意義得
的值;(2)由直線參數(shù)方程幾何意義得![]() ,再將直線
,再將直線![]() 的參數(shù)方程代入拋物線C的普通方程,利用韋達(dá)定理得
的參數(shù)方程代入拋物線C的普通方程,利用韋達(dá)定理得![]() ,
, ![]() , 三個條件聯(lián)立方程組解得
, 三個條件聯(lián)立方程組解得![]() ,即得直線
,即得直線![]() 的普通方程.
的普通方程.
試題解析:(Ⅰ)直線![]() 的普通方程為
的普通方程為![]() ,
,
曲線C的極坐標(biāo)方程可化為![]() ,
,
設(shè)![]() ,
, ![]() ,聯(lián)立
,聯(lián)立![]() 與C的方程得:
與C的方程得: ![]() ,
,
∴![]() ,則
,則![]() ,
,
∴![]() .
.
(Ⅱ)將直線![]() 的參數(shù)方程代入拋物線C的普通方程,
的參數(shù)方程代入拋物線C的普通方程,
得![]() ,
,
設(shè)交點(diǎn)![]() 對應(yīng)的參數(shù)分別為
對應(yīng)的參數(shù)分別為![]() ,
,
則![]() ,
, ![]() ,
,
由![]() 得,
得, ![]() ,
,
聯(lián)立解得![]() ,又
,又![]() ,所以
,所以![]() .
.
直線![]() 的普通方程為
的普通方程為![]() .(或
.(或![]() )
)


 亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案
亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,棱柱ABC﹣A1B1C1的側(cè)面BCC1B1是菱形,B1C⊥A1B 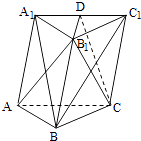
(1)證明:平面AB1C⊥平面A1BC1;
(2)設(shè)D是A1C1上的點(diǎn),且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在2016年龍巖市初中體育中考中,隨意抽取某校5位同學(xué)一分鐘跳繩的次數(shù)分別為:158,160,154,158,170,則由這組數(shù)據(jù)得到的結(jié)論錯誤的是( )
A.平均數(shù)為160
B.中位數(shù)為158
C.眾數(shù)為158
D.方差為20.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱![]() 中,側(cè)面
中,側(cè)面![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).

(Ⅰ)求證:![]() 平面
平面![]() .
.
(Ⅱ)求證:![]() 平面
平面![]() .
.
(Ⅲ)寫出四棱錐![]() 的體積.(只寫出結(jié)論,不需要說明理由)
的體積.(只寫出結(jié)論,不需要說明理由)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖1是某公交公司1路車從起點(diǎn)站A站途經(jīng)B站和C站,最終到達(dá)終點(diǎn)站D站的格點(diǎn)站路線圖.(8×8的格點(diǎn)圖是由邊長為1的小正方形組成)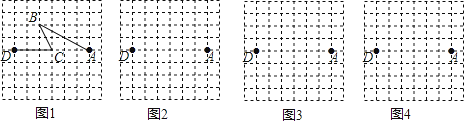
(1)求1路車從A站到D站所走的路程(精確到0.1);
(2)在圖2、圖3和圖4的網(wǎng)格中各畫出一種從A站到D站的路線圖.(要求:①與圖1路線不同、路程相同;②途中必須經(jīng)過兩個格點(diǎn)站;③所畫路線圖不重復(fù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】小麗今天晚自習(xí)準(zhǔn)備復(fù)習(xí)歷史、地理或政治中的一科,她用數(shù)學(xué)游戲的結(jié)果來決定選哪一科,游戲規(guī)則是:在平面直角坐標(biāo)系中,以原點(diǎn)![]() 為起點(diǎn),再分別以
為起點(diǎn),再分別以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 這5個點(diǎn)為終點(diǎn),得到5個向量,任取其中兩個向量,計(jì)算這兩個向量的數(shù)量積
這5個點(diǎn)為終點(diǎn),得到5個向量,任取其中兩個向量,計(jì)算這兩個向量的數(shù)量積![]() ,若
,若![]() ,就復(fù)習(xí)歷史,若
,就復(fù)習(xí)歷史,若![]() ,就復(fù)習(xí)地理,若
,就復(fù)習(xí)地理,若![]() ,就復(fù)習(xí)政治.
,就復(fù)習(xí)政治.
(1)寫出![]() 的所有可能取值;
的所有可能取值;
(2)求小麗復(fù)習(xí)歷史的概率和復(fù)習(xí)地理的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處取得極值.
處取得極值.
(1)討論![]() 和
和![]() 是函數(shù)
是函數(shù)![]() 的極大值還是極小值;
的極大值還是極小值;
(2)過點(diǎn)![]() 作曲線
作曲線![]() 的切線,求此切線方程.
的切線,求此切線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】【河南省豫南九校(中原名校)2017屆高三下學(xué)期質(zhì)量考評八數(shù)學(xué)(文)】已知雙曲線![]() 的左右兩個頂點(diǎn)是
的左右兩個頂點(diǎn)是![]() ,
, ![]() ,曲線
,曲線![]() 上的動點(diǎn)
上的動點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對稱,直線
軸對稱,直線![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,
(1)求動點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)點(diǎn)![]() ,軌跡
,軌跡![]() 上的點(diǎn)
上的點(diǎn)![]() 滿足
滿足![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com