
(本題滿分16分)設二次函數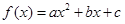 在區間
在區間 上的最大值、最小值分別是
上的最大值、最小值分別是 ,集合
,集合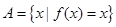 .
.
(1)若 ,且
,且 ,求
,求 和
和 的值;
的值;
(2)若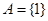 ,且
,且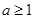 ,記
,記 ,求
,求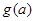 的最小值.
的最小值.
(1)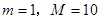 ;(2)
;(2)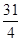 。
。
解析試題分析:由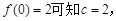 ……………………………1分
……………………………1分
又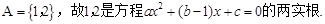
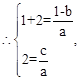 …………………3分
…………………3分 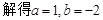 …………4分
…………4分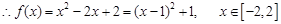
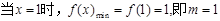 ……………………………5分
……………………………5分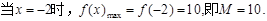 ……………………………6分
……………………………6分
(2)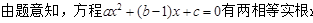 x=1
x=1
∴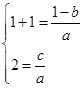 ,即
,即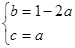 ……………………………8分
……………………………8分
∴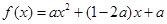 ,
,  ∈[-2,2] , 其對稱軸方程為
∈[-2,2] , 其對稱軸方程為 =
=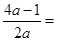
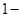
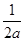
又 ≥1,故1-
≥1,故1-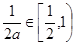 ……………………………9分
……………………………9分
∴M=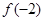 =9
=9 -2, m=
-2, m=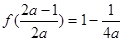
∴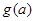 =M+m=9
=M+m=9 -
-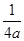 -1 ,…………………………11分
-1 ,…………………………11分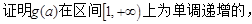 …………………15分
…………………15分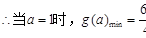 =
=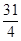 ………16分
………16分
考點:二次函數在閉區間的最值問題。
點評:影響二次函數在閉區間上的最值主要有三個因素:拋物線的開口方向、對稱軸和區間的位置。我們常見的并且感到困難的主要是這兩類問題:一是動軸定區間,二是定軸動區間。


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知集合A={a2,a+1,-3},B={a-3,a2+1,2a-1},若A∩B={-3},
(Ⅰ)求實數a的值.
(Ⅱ)設 ,求不等式
,求不等式 的解集。
的解集。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com