
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數.
上的奇函數.
(1)求![]() 的解析式;
的解析式;
(2)證明:函數![]() 在定義域上是增函數;
在定義域上是增函數;
(3)設![]() 是否存在正實數
是否存在正實數![]() 使得函數
使得函數![]() 在
在![]() 內的最小值為
內的最小值為![]() ?若存在,求出
?若存在,求出![]() 的值;若存在,請說明理由.
的值;若存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 設函數![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)令![]() <
<![]() ≤
≤![]() ,其圖像上任意一點P
,其圖像上任意一點P![]() 處切線的斜率
處切線的斜率![]() ≤
≤![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,方程
時,方程![]() 在區間
在區間![]() 內有唯一實數解,求實數
內有唯一實數解,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F為棱BB1的中點,M為線段AC1的中點.

(1)求證:直線MF∥平面ABCD;
(2)求證:平面AFC1⊥平面ACC1A1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】信息科技的進步和互聯網商業模式的興起,全方位地改變了大家金融消費的習慣和金融交易模式,現在銀行的大部分業務都可以通過智能終端設備完成,多家銀行職員人數在悄然減少.某銀行現有職員320人,平均每人每年可創利20萬元.據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利0.2萬元,但銀行需付下崗職員每人每年6萬元的生活費,并且該銀行正常運轉所需人數不得小于現有職員的![]() ,為使裁員后獲得的經濟效益最大,該銀行應裁員多少人?此時銀行所獲得的最大經濟效益是多少萬元?
,為使裁員后獲得的經濟效益最大,該銀行應裁員多少人?此時銀行所獲得的最大經濟效益是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(Ⅰ)求橢圓![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是橢圓
是橢圓![]() 上兩個不同的動點,且使
上兩個不同的動點,且使![]() 的角平分線垂直于
的角平分線垂直于![]() 軸,試判斷直線
軸,試判斷直線![]() 的斜率是否為定值?若是,求出該值;若不是,說明理由.
的斜率是否為定值?若是,求出該值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
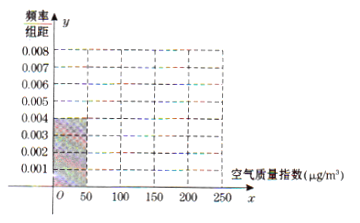
【題目】全世界越來越關注環境保護問題,某省一監測站點于2016年8月某日起連續![]() 天監測空氣質量指數
天監測空氣質量指數![]() ,數據統計如下:
,數據統計如下:

(Ⅰ)根據所給統計表和頻率分布直方圖中的信息求出![]() 、
、![]() 的值,并完成頻率分布直方圖;
的值,并完成頻率分布直方圖;
(Ⅱ)在空氣質量指數分別為![]() 和
和![]() 的監測數據中,用分層抽樣的方法抽取5天,從中任意選取2天,求事件
的監測數據中,用分層抽樣的方法抽取5天,從中任意選取2天,求事件![]() “兩天空氣都為良”發生的概率.
“兩天空氣都為良”發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)若曲線![]() 在
在![]() 軸上的截距為-1,且在點
軸上的截距為-1,且在點![]() 處的切線垂直于直線
處的切線垂直于直線![]() ,求實數
,求實數![]() 的值;
的值;
(Ⅱ)記![]() 的導函數為
的導函數為![]() ,
, ![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行漢字聽寫比賽,為了了解本次比賽成績情況,從得分不低于50分的試卷中隨機抽取100名學生的成績(得分均為整數,滿分100分)進行統計,請根據頻率分布表中所提供的數據,解答下列問題:
組號 | 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 5 | 0.05 |
第2組 | [60,70) |
| 0.35 |
第3組 | [70,80) | 30 |
|
第4組 | [80,90) | 20 | 0.20 |
第5組 | [90,100] | 10 | 0.10 |
合計 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若從成績較好的第3、4、5組中按分層抽樣的方法抽取6人參加市漢字聽寫比賽,并從中選出2人做種子選手,求2人中至少有1人是第4組的概率。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com