
如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,![]() ,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,點F是AE的中點。
,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,點F是AE的中點。

(1)證明:DF∥平面ABC;
(2)求AB與平BDF所成角的大小。
解:(1)取AB的中點G,連CG,GF,如圖a所示。

則GF∥BE,且![]() ,
,
∴GF∥CD,且GF=CD。
∴四邊形FGCD是平行四邊形。
∴GF∥CG,又![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴DF∥平面ABC。
(2)解法一:設A到平面BDF的距離為![]() ,
,
由![]() 得
得![]()
在![]() 中,
中,![]() ,
,
∴![]() ,又
,又![]() ,且
,且![]() ,
,
∴
又設AB與平面BDF所成的角為![]() ,則
,則 ,
,
故AB與平面BDF所成的角為![]() 。
。
解法二:以點B為原點,BA、BC、BE所在的直線分別為![]() 、
、![]() 、
、![]() 軸,
軸,
建立如圖b所示的空間直角坐標

系,則B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1),
E(0,0,2),F(1,0,1).
![]()
設平面BDF的一個法向量為![]() ,
,
∵![]()
∴
即![]() ,解得
,解得![]()
∴![]() 。
。
又設AB與平面BDF所成的角為![]() ,則法線
,則法線![]() 與
與![]() 所成的角為
所成的角為![]() ,
,
∴ ,即
,即![]()
故AB與平面BDF所成的角為![]() 。
。


科目:高中數學 來源: 題型:
 如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,點F是AE的中點.
如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,點F是AE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,F是AE的中點.
如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,F是AE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•合肥一模)如圖,在多面體ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如圖,在多面體ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
| ||
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年新建二中模擬)如圖,在幾何體ABCDE中,△ABC是等腰直角三角形,∠ABC = 90°,BE和CD都垂直于平面ABC,且BE = AB = 2,CD = 1,點F是AE的中點.
(1)求證:DF∥平面ABC;
(2)求AB與平面BDF所成角的大小.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省濰坊市高三上學期期末考試文科數學試卷(解析版) 題型:解答題
如圖,在幾何體 中,點
中,點 在平面ABC內的正投影分別為A,B,C,且
在平面ABC內的正投影分別為A,B,C,且 ,E為
,E為 中點,
中點, .
.

(1)求證;CE∥平面 ,
,
(2)求證:平面 平面
平面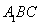
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com