
【題目】已知函數f(x)=![]() 的圖像在點M(-1,f(-1))處的切線方程為x+2y+5=0,
的圖像在點M(-1,f(-1))處的切線方程為x+2y+5=0,
(1)求函數y=f(x)的解析式;
(2)求函數y=f(x)的單調區間.
【答案】(1)![]() ;(2)單調遞增區間是(3-2
;(2)單調遞增區間是(3-2![]() ,3+2
,3+2![]() );單調遞減區間是(-∞,3-2
);單調遞減區間是(-∞,3-2![]() )和(3+2
)和(3+2![]() ,+∞).
,+∞).
【解析】試題分析:(1)先求出函數導數,由切線斜率得在點x=-1的斜率,再由f(-1)=-2帶入函數即可求解析式;
(2)令導數大于0得增區間,令導數小于0得減區間.
試題解析:
(1)由函數f(x)的圖像在點M(-1,f(-1))處的切線方程為x+2y+5=0,
知f′(-1)=-![]() ,且-1+2f(-1)+5=0,
,且-1+2f(-1)+5=0,
即f(-1)=-2,![]() =-2,①
=-2,①
又f′(x)=![]() ,
,
所以![]() =-
=-![]() .②
.②
由①②得a=2,b=3.
(因為b+1≠0, 所以b=-1舍去)
所以所求函數解析式是f(x)=![]() .
.
(2)由(1)可得f′(x)=![]() .
.
令-2x2+12x+6=0,解得x1=3-2![]() ,x2=3+2
,x2=3+2![]() ,
,
則當x<3-2![]() 或x>3+2
或x>3+2![]() 時,f′(x)<0,
時,f′(x)<0,
當3-2![]() <x<3+2
<x<3+2![]() 時,f′(x)>0,
時,f′(x)>0,
所以f(x)=![]() 的單調遞增區間是(3-2
的單調遞增區間是(3-2![]() ,3+2
,3+2![]() );
);
單調遞減區間是(-∞,3-2![]() )和(3+2
)和(3+2![]() ,+∞).
,+∞).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{xn}滿足x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ為非零常數,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比數列,求λ的值;
(λ為非零常數,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比數列,求λ的值;
(Ⅱ)設0<λ<1,常數k∈N* , 證明 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2015高考山東文數】某中學調查了某班全部![]() 名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
參加書法社團 | 未參加書法社團 | |
參加演講社團 |
|
|
未參加演講社團 |
|
|
(1)從該班隨機選![]() 名同學,求該同學至少參加上述一個社團的概率;
名同學,求該同學至少參加上述一個社團的概率;
(2)在既參加書法社團又參加演講社團的![]() 名同學中,有5名男同學
名同學中,有5名男同學![]()
![]() 名女同學
名女同學![]() 現從這
現從這![]() 名男同學和
名男同學和![]() 名女同學中各隨機選
名女同學中各隨機選![]() 人,求
人,求![]() 被選中且
被選中且![]() 未被選中的概率.
未被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
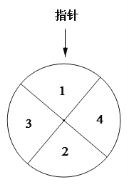
【題目】【2016高考山東文數】某兒童樂園在“六一”兒童節推出了一項趣味活動.參加活動的兒童需轉動如圖所示的轉盤兩次,每次轉動后,待轉盤停止轉動時,記錄指針所指區域中的數.設兩次記錄的數分別為x,y.獎勵規則如下:
①若![]() ,則獎勵玩具一個;
,則獎勵玩具一個;
②若![]() ,則獎勵水杯一個; ③其余情況獎勵飲料一瓶.
,則獎勵水杯一個; ③其余情況獎勵飲料一瓶.
假設轉盤質地均勻,四個區域劃分均勻.小亮準備參加此項活動.
(I)求小亮獲得玩具的概率;
(II)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】來自某校一班和二班的共計9名學生志愿服務者被隨機平均分配到運送礦泉水、清掃衛生、維持秩序這三個崗位服務,且運送礦泉水崗位至少有一名一班志愿者的概率是![]() .
.
(Ⅰ)求清掃衛生崗位恰好一班1人、二班2人的概率;
(Ⅱ)設隨機變量![]() 為在維持秩序崗位服務的一班的志愿者的人數,求
為在維持秩序崗位服務的一班的志愿者的人數,求![]() 分布列及期望.
分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某地區某高傳染性病毒流行期間,為了建立指標顯示疫情已受控制,以便向該地區居眾顯示可以過正常生活,有公共衛生專家建議的指標是“連續7天每天新增感染人數不超過5人”,根據連續7天的新增病倒數計算,下列各選項中,一定符合上述指標的是( )
①平均數 ![]() ;
;
②標準差S≤2;
③平均數 ![]() 且標準差S≤2;
且標準差S≤2;
④平均數 ![]() 且極差小于或等于2;
且極差小于或等于2;
⑤眾數等于1且極差小于或等于1.
A.①②
B.③④
C.③④⑤
D.④⑤
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com