
 如圖所示為某風景區設計建造的一個休閑廣場,廣場的中間造型的平面圖是由兩個相同的矩形ABCD和EFGH構成對稱的十字形區域,十字形區域面積為2000m2,計劃在正方方形MNPQ上建一座“觀景花壇”,造價為每平方4100元,在四個相同的矩形上(圖中陰影部分)鋪石材地坪,價格為每平方110元,再在四個空角(如△DQH等)上鋪草坪,價格為每平方80元.設AD長為xm,DQ長為ym.
如圖所示為某風景區設計建造的一個休閑廣場,廣場的中間造型的平面圖是由兩個相同的矩形ABCD和EFGH構成對稱的十字形區域,十字形區域面積為2000m2,計劃在正方方形MNPQ上建一座“觀景花壇”,造價為每平方4100元,在四個相同的矩形上(圖中陰影部分)鋪石材地坪,價格為每平方110元,再在四個空角(如△DQH等)上鋪草坪,價格為每平方80元.設AD長為xm,DQ長為ym. ,
,
 ≤20
≤20
 )2
)2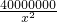 +180000
+180000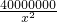 +180000,再利用基本不等式 求解即可.
+180000,再利用基本不等式 求解即可.

科目:高中數學 來源: 題型:
 如圖所示為某風景區設計建造的一個休閑廣場,廣場的中間造型的平面圖是由兩個相同的矩形ABCD和EFGH構成對稱的十字形區域,十字形區域面積為2000m2,計劃在正方方形MNPQ上建一座“觀景花壇”,造價為每平方4100元,在四個相同的矩形上(圖中陰影部分)鋪石材地坪,價格為每平方110元,再在四個空角(如△DQH等)上鋪草坪,價格為每平方80元.設AD長為xm,DQ長為ym.
如圖所示為某風景區設計建造的一個休閑廣場,廣場的中間造型的平面圖是由兩個相同的矩形ABCD和EFGH構成對稱的十字形區域,十字形區域面積為2000m2,計劃在正方方形MNPQ上建一座“觀景花壇”,造價為每平方4100元,在四個相同的矩形上(圖中陰影部分)鋪石材地坪,價格為每平方110元,再在四個空角(如△DQH等)上鋪草坪,價格為每平方80元.設AD長為xm,DQ長為ym.查看答案和解析>>
科目:高中數學 來源: 題型:
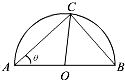 某風景區在一個直徑AB為100米的半圓形花園中設計一條觀光線路(如圖所示).在點A與圓弧上的一點C之間設計為直線段小路,在路的兩側邊緣種植綠化帶;從點C到點B設計為沿弧的弧形小路,在路的一側邊緣種植綠化帶.(注:小路及綠化帶的寬度忽略不計)
某風景區在一個直徑AB為100米的半圓形花園中設計一條觀光線路(如圖所示).在點A與圓弧上的一點C之間設計為直線段小路,在路的兩側邊緣種植綠化帶;從點C到點B設計為沿弧的弧形小路,在路的一側邊緣種植綠化帶.(注:小路及綠化帶的寬度忽略不計)查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省無錫市高一(下)期末數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com