
 如圖所示的數表,對任意正整數i(i=1,2,3,…)滿足以下兩個條件:
如圖所示的數表,對任意正整數i(i=1,2,3,…)滿足以下兩個條件:| n3-n2+2n |
| 2 |
| n3-n2+2n |
| 2 |
| an-1 |
| n-1 |
| an-1 |
| n-1 |
| an-1 |
| n-1 |
| an-1 |
| n-1 |
| an |
| n |
| n(n-1) |
| 2 |
| an-1 |
| n-1 |
| (n-1)(n-2) |
| 2 |
| an |
| n |
| n(n-1) |
| 2 |
| an-1 |
| n-1 |
| (n-1)(n-2) |
| 2 |
| a1 |
| 1 |
| n3-n2+2n |
| 2 |
| a6 |
| 6 |
| 96 |
| 6 |
| n3-n2+2n |
| 2 |


科目:高中數學 來源:2012年全國普通高等學校招生統一考試文科數學(北京卷解析版) 題型:解答題
設A是如下形式的2行3列的數表,
|
a |
b |
c |
|
d |
e |
f |
滿足性質P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
記 為A的第i行各數之和(i=1,2),
為A的第i行各數之和(i=1,2),  為A的第j列各數之和(j=1,2,3)記
為A的第j列各數之和(j=1,2,3)記 為
為 中的最小值。
中的最小值。
(1)對如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)設數表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)對所有滿足性質P的2行3列的數表A,求 的最大值。
的最大值。
【解析】(1)因為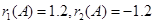 ,
, ,所以
,所以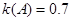
(2)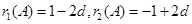 ,
,
因為 ,所以
,所以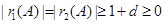 ,
,
所以
當d=0時, 取得最大值1
取得最大值1
(3)任給滿足性質P的數表A(如圖所示)
|
a |
b |
c |
|
d |
e |
f |
任意改變A的行次序或列次序,或把A中的每個數換成它的相反數,所得數表 仍滿足性質P,并且
仍滿足性質P,并且 ,因此,不妨設
,因此,不妨設 ,
, ,
,
由 得定義知,
得定義知, ,
, ,
, ,
,
從而

所以, ,由(2)知,存在滿足性質P的數表A使
,由(2)知,存在滿足性質P的數表A使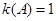 ,故
,故 的最大值為1
的最大值為1
【考點定位】此題作為壓軸題難度較大,考查學生分析問題解決問題的能力,考查學生嚴謹的邏輯思維能力
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com