
設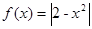 ,若
,若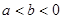 ,且
,且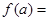
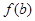 ,則
,則 的取值范圍是
的取值范圍是
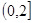
【解析】
試題分析:由于a,b小于0,所以只需研究x<0的函數的性質,利用絕對值的意義去掉絕對值符號,得到分段函數;當x<0時,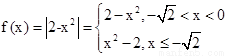 ,然后結合二次函數的
心智可知
,然后結合二次函數的
心智可知
∴f(x)在(-∞,-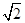 )遞減;在(-
)遞減;在(-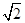 ,0)遞增
,0)遞增
∵a<b<0,且f(a)=f(b),代入解析式得到a,b的范圍
∴a≤-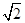 ,0>b>-
,0>b>-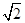 且a2-2=- a2+2,解得a=-
且a2-2=- a2+2,解得a=-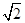 ;-
;-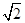 <b<0,∴0<ab<2
<b<0,∴0<ab<2
考點:本題考查利用絕對值的意義去掉絕對值符號,將絕對值函數轉化為不含絕對值的函數、考查不等式的性質.
點評:解決該試題的關鍵是根據a,b小于0,所以只需研究x<0的函數的性質,利用絕對值的意義去掉絕對值符號,得到分段函數;得到f(x)在x<0上的單調性;判斷出a,b的范圍,利用f(a)=f(b),列出方程求出a的值,求出ab的范圍.


 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com