
(14分)已知函數(shù) ,其中a是實數(shù).設(shè)A(x1,f(x1)),B(x2,f(x2))為該函數(shù)圖象上的兩點,且x1<x2.
,其中a是實數(shù).設(shè)A(x1,f(x1)),B(x2,f(x2))為該函數(shù)圖象上的兩點,且x1<x2.
(Ⅰ)指出函數(shù)f(x)的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)f(x)的圖象在點A,B處的切線互相垂直,且x2<0,證明:x2﹣x1≥1;
(Ⅲ)若函數(shù)f(x)的圖象在點A,B處的切線重合,求a的取值范圍.
(Ⅰ)函數(shù)f(x)的單調(diào)減區(qū)間(﹣∞,﹣1),函數(shù)f(x)的單調(diào)增區(qū)間[﹣1,0),(0,+∞)
(Ⅱ)見解析
(Ⅲ)(﹣ln2﹣1,+∞)
【解析】(I)函數(shù)f(x)的單調(diào)減區(qū)間(﹣∞,﹣1),函數(shù)f(x)的單調(diào)增區(qū)間[﹣1,0),(0,+∞);
(II)由導(dǎo)數(shù)的幾何意義知,點A處的切線的斜率為f′(x1),點B處的切線的斜率為f′(x2),
函數(shù)f(x)的圖象在點A,B處的切線互相垂直時,有f′(x1)f′(x2)=﹣1,
當x<0時,(2x1+2)(2x2+2)=﹣1,∵x1<x2<0,∴2x1+2<0,2x2+2>0,
∴x2﹣x1=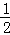 [﹣(2x1+2)+(2x2+2)]≥
[﹣(2x1+2)+(2x2+2)]≥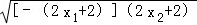 =1,
=1,
∴若函數(shù)f(x)的圖象在點A,B處的切線互相垂直,有x2﹣x1≥1;
(III)當x1<x2<0,或0<x1<x2時,f′(x1)≠f′(x2),故x1<0<x2,
當x1<0時,函數(shù)f(x)在點A(x1,f(x1))處的切線方程為y﹣(x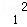 +2x1+a)=(2x1+2)(x﹣x1);
+2x1+a)=(2x1+2)(x﹣x1);
當x2>0時,函數(shù)f(x)在點B(x2,f(x2))處的切線方程為y﹣lnx2=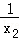 (x﹣x2);
(x﹣x2);
兩直線重合的充要條件是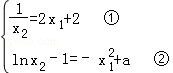 ,
,
由①及x1<0<x2得0<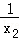 <2,由①②得a=lnx2+(
<2,由①②得a=lnx2+(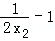 )2﹣1=﹣ln
)2﹣1=﹣ln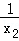 +
+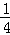 (
(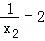 )2﹣1,
)2﹣1,
令t=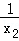 ,則0<t<2,且a=
,則0<t<2,且a=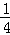 t2﹣t﹣lnt,設(shè)h(t)=
t2﹣t﹣lnt,設(shè)h(t)=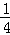 t2﹣t﹣lnt,(0<t<2)
t2﹣t﹣lnt,(0<t<2)
則h′(t)=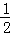 t﹣1﹣
t﹣1﹣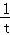 =
=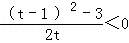 ,∴h(t)在(0,2)為減函數(shù),
,∴h(t)在(0,2)為減函數(shù),
則h(t)>h(2)=﹣ln2﹣1,∴a>﹣ln2﹣1,
∴若函數(shù)f(x)的圖象在點A,B處的切線重合,a的取值范圍(﹣ln2﹣1,+∞).


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學(xué)課時作業(yè)系列答案
名牌中學(xué)課時作業(yè)系列答案 明天教育課時特訓(xùn)系列答案
明天教育課時特訓(xùn)系列答案 浙江新課程三維目標測評課時特訓(xùn)系列答案
浙江新課程三維目標測評課時特訓(xùn)系列答案科目:高中數(shù)學(xué) 來源: 題型:
| π |
| 6 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 已知函數(shù)
已知函數(shù)![]() ,其中a,b為實常數(shù).
,其中a,b為實常數(shù).
(Ⅰ)求函數(shù)![]() 為奇函數(shù)的充要條件;
為奇函數(shù)的充要條件;
(Ⅱ)若任取a∈[0,4],b∈[0,3],求函數(shù)![]() 在R上是增函數(shù)的概率.
在R上是增函數(shù)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年北京市西城區(qū)高三二模理科數(shù)學(xué)試卷(解析版) 題型:選擇題
已知函數(shù)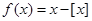 ,其中
,其中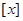 表示不超過實數(shù)
表示不超過實數(shù)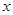 的最大整數(shù).若關(guān)于
的最大整數(shù).若關(guān)于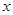 的方程
的方程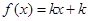 有三個不同的實根,則實數(shù)
有三個不同的實根,則實數(shù)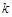 的取值范圍是( )
的取值范圍是( )
(A)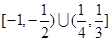 (B)
(B)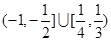
(C)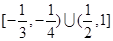 (D)
(D)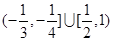
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
| π |
| 6 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2009-2010學(xué)年江蘇省南通中學(xué)高二(下)期末數(shù)學(xué)模擬試卷(理科)(解析版) 題型:填空題
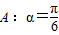 ,
,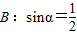 ;(2)A:x=1,B:x2+(a2-1)x-a2=0(a為實常數(shù));(3)A:定義域為R上的函數(shù)f(x)滿足f(1)>f(2),B:定義域為R的函數(shù)f(x)是單調(diào)減函數(shù).其中A是B的充分不必要條件的是 .(填寫所有滿足要求的條件組的序號)
;(2)A:x=1,B:x2+(a2-1)x-a2=0(a為實常數(shù));(3)A:定義域為R上的函數(shù)f(x)滿足f(1)>f(2),B:定義域為R的函數(shù)f(x)是單調(diào)減函數(shù).其中A是B的充分不必要條件的是 .(填寫所有滿足要求的條件組的序號)查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com