
【題目】如圖,在正四棱錐![]() 中,
中,![]() ,
,![]() .
.
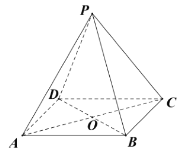
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC-A1B1C1中,側面BCC1B1是菱形,AC=BC=2,∠CBB1=![]() ,點A在平面BCC1B1上的投影為棱BB1的中點E.
,點A在平面BCC1B1上的投影為棱BB1的中點E.
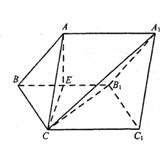
(1)求證:四邊形ACC1A1為矩形;
(2)求二面角E-B1C-A1的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省級示范高中高三年級對各科考試的評價指標中,有“難度系數“和“區分度“兩個指標中,難度系數![]() ,區分度
,區分度![]() .
.
(1)某次數學考試(滿分為150分),隨機從實驗班和普通班各抽取三人,實驗班三人的成績分別為147,142,137;普通班三人的成績分別為97,102,113.通過樣本估計本次考試的區分度(精確0.01).
(2)如表表格是該校高三年級6次數學考試的統計數據:
難度系數x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
區分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①計算相關系數r,|r|<0.75時,認為相關性弱;|r|≥0.75時,認為相關性強.通過計算說明,能否利用線性回歸模型描述y與x的關系(精確到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y關于t的線性回歸方程,并預測x=0.75時y的值(精確到0.01).
附注:參考數據: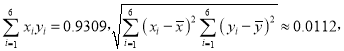
![]()
![]()
參考公式:相關系數 r,回歸直線
r,回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點
的中點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)已知點![]() ,過點
,過點![]() 作直線
作直線![]() 交拋物線于
交拋物線于![]() 、
、![]() 兩點,求
兩點,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值時直線
取得最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 的準線上一點,F為拋物線的焦點,P為拋物線上的點,且
的準線上一點,F為拋物線的焦點,P為拋物線上的點,且![]() ,若雙曲線C中心在原點,F是它的一個焦點,且過P點,當m取最小值時,雙曲線C的離心率為______.
,若雙曲線C中心在原點,F是它的一個焦點,且過P點,當m取最小值時,雙曲線C的離心率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶節期間,滕州市實驗小學舉行了一次科普知識競賽活動,設置了一等獎、二等獎、三等獎、四等獎及紀念獎,獲獎人數的分配情況如圖所示,各個獎品的單價分別為:一等獎50元、二等獎20元、三等獎10元,四等獎5元,紀念獎2元,則以下說法中不正確的是( )
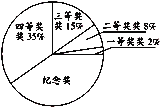
A.獲紀念獎的人數最多B.各個獎項中二等獎的總費用最高
C.購買獎品的費用平均數為6.65元D.購買獎品的費用中位數為5元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市組織高三全體學生參加計算機操作比賽,等級分為1至10分,隨機調閱了A、B兩所學校各60名學生的成績,得到樣本數據如下:
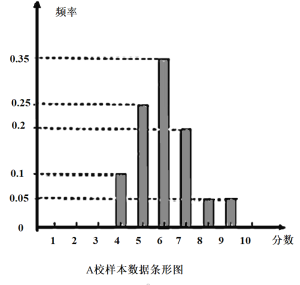
B校樣本數據統計表:
成績(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人數(個) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)計算兩校樣本數據的均值和方差,并根據所得數據進行比較.
(2)從A校樣本數據成績分別為7分、8分和9分的學生中按分層抽樣方法抽取6人,若從抽取的6人中任選2人參加更高一級的比賽,求這2人成績之和大于或等于15的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)當m=1時,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com