【題目】若樣本
的平均數是
，方差是
，則對樣本
，下列結論正確的是 ( )
A. 平均數為14，方差為5 B. 平均數為13，方差為25
C. 平均數為13，方差為5 D. 平均數為14，方差為2
【答案】C
【解析】
根據平均數和方差的定義和性質進行求解即可．
∵樣本1+x1，1+x2，1+x3，…，1+xn的平均數是12，方差為5，
∴1+x1+1+x2+1+x3+…+1+xn=12n，
即x1+x2+x3+…+xn=12n﹣n=11n，
方差S2=
[（1+x1﹣12）2+（1+x2﹣12）2+…+（1+xn﹣12）2]=[（x1﹣11）2+（x2﹣11）2+…+（xn﹣11）2]=5，
則（2+x1+2+x2+…+2+xn）=
=13，
樣本2+x1，2+x2，…，2+xn的方差S2=[（2+x1﹣13）2+（2+x2﹣13）2+…+（2+xn﹣13）2]
=[（x1﹣11）2+（x2﹣11）2+…+（xn﹣11）2]=5，
故選：C．
寒假樂園北京教育出版社系列答案科目：高中數學 來源： 題型：
【題目】若命題p：函數y=x2﹣2x的單調遞增區間是[1，+∞），命題q：函數y=x﹣ 
的單調遞增區間是[1，+∞），則（ ）
A.p∧q是真命題
B.p∨q是假命題
C.非p是真命題
D.非q是真命題
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知不等式
的解集為(1，t)，記函數
.
(1)求證：函數y＝f(x)必有兩個不同的零點；
(2)若函數y＝f(x)的兩個零點分別為
，
，試將
表示成以
為自變量的函數，并求的取值范圍；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cosx+sinx，2sinx）， 
=（cosx﹣sinx，cosx）．令f（x）= ．
（1）求f（x）的最小正周期；
（2）求f（x）在[ 
， 
]上的單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設關于x的一元二次方程
，其中a，b是某范圍內的隨機數，分別在下列條件下，求上述方程有實根的概率．
(1)若隨機數a，b∈{1,2,3,4,5,6}；
(2)若a是從區間[0,5]中任取的一個數，b是從區間[2,4]中任取的一個數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是我國2008年至2014年生活垃圾無害化處理量（單位：億噸）的折線圖.
（Ⅰ）由折線圖看出，可用線性回歸模型擬合y與t的關系，請用相關系數加以說明；
（Ⅱ）建立y關于t的回歸方程（系數精確到0.01），預測2016年我國生活垃圾無害化處理量.
附注：
參考數據：
，
，
，
≈2.646.
參考公式：相關系數
回歸方程
中斜率和截距的最小二乘估計公式分別為：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】閱讀如圖所示的程序框圖，則該算法的功能是（ ）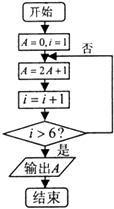 
A.計算數列{2n﹣1}前5項的和
B.計算數列{2n﹣1}前5項的和
C.計算數列{2n﹣1}前6項的和
D.計算數列{2n﹣1}前6項的和
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）=ax3﹣3x2+1（a＞0），定義h（x）=max{f（x），g（x）}= 
．
（1）求函數f（x）的極值；
（2）若g（x）=xf'（x），且存在x∈[1，2]使h（x）=f（x），求實數a的取值范圍；
（3）若g（x）=lnx，試討論函數h（x）（x＞0）的零點個數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
