

(1)若數列{an}是首項為1,公差為2的等差數列,寫出圖中第5行第5個數;
(2)若函數f(x)=a1x+a2x2+a3x3+…+anxn,且f(1)= n2,求數列{an}的通項公式;
(3)設Tm為第m行所有項的和,在(2)的條件下,用含m的代數式表示Tm.
解:(1)第5行第5個數是29.
(2)由f(1)=n2,得a1+a2+a3+…+an=n2.
設Sn是數列{an}的前n項和,∴Sn=n2.當n=1時,a1=S1=1,
當n≥2時,an=Sn-Sn-1=n2-(n-1)2=2n-1.
又當n=1時,2n-1=1=a1,∴an=2n-1,
即數列{an}的通項公式是an=2n-1(n=1,2,3,…).
(3)由(2)知數列{an}是首項為1,公差為2的等差數列.
∵前m-1行共有項1+2+3+…+(m-1)=![]() ×(m-1)=
×(m-1)=![]() ,
,
∴第m行的第一項為![]() +1=2×(
+1=2×(![]() +1)-1=m2-m+1.
+1)-1=m2-m+1.
∴第m行構成首項為m2-m+1,公差為2的等差數列,且有m項.
∴Tm=(m2-m+1)×m+![]() ×2=m3.
×2=m3.


科目:高中數學 來源: 題型:
 將數列{an}的各項排成如圖所示的三角形形狀.
將數列{an}的各項排成如圖所示的三角形形狀.查看答案和解析>>
科目:高中數學 來源: 題型:
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
(1)求數列{an}的通項公式;
(2)將數列{an}的各項排成三角形狀(如圖),記A(i,j)為第i行第j個數,例如:A(4,3)=a9,求A(10,1)+A(10,2)+…+A(10,10);
(3)若bn=![]() ,cn=
,cn=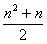 ,Tn為數列{cn}的前n項和,若Tn<λ(bn+1+1),對一切n∈N*都成立,試求λ的取值范圍.
,Tn為數列{cn}的前n項和,若Tn<λ(bn+1+1),對一切n∈N*都成立,試求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省南昌市高三(上)期中數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省南昌市高三(上)期中數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:2008年北京市海淀區高考數學二模試卷(文科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com