

【題目】“中國式過馬路”存在很大的交通安全隱患,某調(diào)查機(jī)構(gòu)為了解路人對“中國式過馬路”的態(tài)度是否與性別有關(guān),從馬路旁隨機(jī)抽取30名路人進(jìn)行了問卷調(diào)查,得到了如圖的![]() 列聯(lián)表.已知在這30人中隨機(jī)抽取1人抽到反感“中國式過馬路”的路人的概率是
列聯(lián)表.已知在這30人中隨機(jī)抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)求![]() 列聯(lián)表中的
列聯(lián)表中的![]() ,
,![]() 的值;
的值;
男性 | 女性 | 合計 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合計 |
|
| 30 |
(2)根據(jù)列聯(lián)表中的數(shù)據(jù),判斷是否有95%把握認(rèn)為反感“中國式過馬路”與性別有關(guān)?
臨界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
參考公式: ,
,![]()
 陽光課堂課時作業(yè)系列答案
陽光課堂課時作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中央政府為了應(yīng)對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”.為了了解人們]對“延遲退休年齡政策”的態(tài)度,責(zé)成人社部進(jìn)行調(diào)研.人社部從網(wǎng)上年齡在15∽65歲的人群中隨機(jī)調(diào)查100人,調(diào)査數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結(jié)果如下:
年齡 |
|
|
|
|
|
支持“延遲退休”的人數(shù) | 15 | 5 | 15 | 28 | 17 |
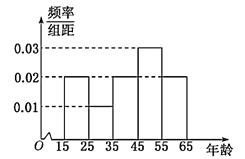
(1)由以上統(tǒng)計數(shù)據(jù)填![]() 列聯(lián)表,并判斷能否在犯錯誤的概率不超過0.05的前提下認(rèn)為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
列聯(lián)表,并判斷能否在犯錯誤的概率不超過0.05的前提下認(rèn)為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
45歲以下 | 45歲以上 | 總計 | |
支持 | |||
不支持 | |||
總計 |
(2)若以45歲為分界點,從不支持“延遲退休”的人中按分層抽樣的方法抽取8人參加某項活動.現(xiàn)從這8人中隨機(jī)抽2人
①抽到1人是45歲以下時,求抽到的另一人是45歲以上的概率.
②記抽到45歲以上的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
參考數(shù)據(jù):
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖為我國數(shù)學(xué)家趙爽![]() 約3世紀(jì)初
約3世紀(jì)初![]() 在為《周髀算經(jīng)》作注時驗證勾股定理的示意圖,現(xiàn)在提供5種顏色給其中5個小區(qū)域涂色,規(guī)定每個區(qū)域只涂一種顏色,相鄰區(qū)域顏色不同,則
在為《周髀算經(jīng)》作注時驗證勾股定理的示意圖,現(xiàn)在提供5種顏色給其中5個小區(qū)域涂色,規(guī)定每個區(qū)域只涂一種顏色,相鄰區(qū)域顏色不同,則![]() 區(qū)域涂色不相同的概率為
區(qū)域涂色不相同的概率為![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知常數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)討論![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性;
上的單調(diào)性;
(2)若![]() 存在兩個極值點
存在兩個極值點![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.
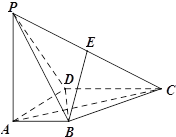
(1)證明:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 為棱
為棱![]() 上一點,滿足
上一點,滿足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位對員工業(yè)務(wù)進(jìn)行考核,從![]() 類員工(工作3年及3年以內(nèi)的員工)和
類員工(工作3年及3年以內(nèi)的員工)和![]() 類員工(工作3年以上的員工)的成績中各抽取15個,具體數(shù)據(jù)如下:
類員工(工作3年以上的員工)的成績中各抽取15個,具體數(shù)據(jù)如下:

![]() 類成績:20 10 22 30 15 12 41 22 31 25 12 26 29 32 33
類成績:20 10 22 30 15 12 41 22 31 25 12 26 29 32 33
![]() 類成績:21 40 30 41 42 31 49 51 52 43 47 47 32 45 48
類成績:21 40 30 41 42 31 49 51 52 43 47 47 32 45 48
(1)根據(jù)兩組數(shù)據(jù)完成兩類員工成績的莖葉圖,并通過莖葉圖比較兩類員工成績的平均值及分散程度(不要求計算出具體值,得出結(jié)論即可);
(2)研究發(fā)現(xiàn)從業(yè)時間與業(yè)務(wù)能力之間具有線性相關(guān)關(guān)系,從上述抽取的![]() 名員工中抽取4名員工的成績?nèi)缦拢?/span>
名員工中抽取4名員工的成績?nèi)缦拢?/span>
員工工作時間 | 1 | 2 | 3 | 4 |
考核成績 | 10 | 15 | 20 | 30 |
根據(jù)四個的數(shù)據(jù),求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程.
的線性回歸方程.
附:回歸直線![]() 的斜率和截距的最小二乘法估計公式分別為:
的斜率和截距的最小二乘法估計公式分別為: ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,且
,且![]() ,橢圓經(jīng)過點
,橢圓經(jīng)過點![]() .
.
(1)求橢圓的方程;
(2)直線![]() 過橢圓右頂點
過橢圓右頂點![]() ,交橢圓于另一點
,交橢圓于另一點![]() ,點
,點![]() 在直線
在直線![]() 上,且
上,且![]() .若
.若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 上一點,
上一點,![]() 為
為![]() 的中點,且
的中點,且![]() ,
,![]() ,現(xiàn)將梯形沿
,現(xiàn)將梯形沿![]() 折疊(如圖2),使平面
折疊(如圖2),使平面![]() 平面
平面![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() .
.
(2)能否在邊![]() 上找到一點
上找到一點![]() (端點除外)使平面
(端點除外)使平面![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() ?若存在,試確定點
?若存在,試確定點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() 分別為雙曲線
分別為雙曲線![]()
![]()
![]() 的左、右焦點,點P是以
的左、右焦點,點P是以![]() 為直徑的圓與C在第一象限內(nèi)的交點,若線段
為直徑的圓與C在第一象限內(nèi)的交點,若線段![]() 的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com