
(本題10分) 為了讓學生了解環保知識,增強環保意識,某中學舉行了一次“環保知識競賽”,共有900名學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了部分學生的成績(得分均為整數,滿分為100分)進行統計.請你根據尚未完成并有局部污損的頻率分布表和頻率分布直方圖,解答下列問題:
|
分組 |
頻數 |
頻率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
|
|
|
合計 |
50 |
|

(Ⅰ)填充頻率分布表的空格(將答案直接填在表格內);
(Ⅱ)補全頻率分布直方圖;
(Ⅲ)學校決定成績在75.5~85.5分的學生為二等獎,
問該校獲得二等獎的學生約為多少人?
略
【解析】解:(1) ——3分
|
分組 |
頻數 |
頻率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
8 |
0.16 |
|
70.5~80.5 |
10 |
0.20 |
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
12 |
0.24 |
|
合計 |
50 |
1.00 |
(2)頻率分布直方圖如右上所示:——3分
(3)成績在75.5~80.5分的學生占70.5~80.5分的學生的 ,因為成績在70.5~80.5分的學生頻率為0.2 ,所以成績在76.5~80.5分的學生頻率為0.1 ,
,因為成績在70.5~80.5分的學生頻率為0.2 ,所以成績在76.5~80.5分的學生頻率為0.1 ,
成績在80.5~85.5分的學生占80.5~90.5分的學生的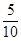 ,因為成績在80.5~90.5分的學生頻率為0.32 ,所以成績在80.5~85.5分的學生頻率為0.16
,因為成績在80.5~90.5分的學生頻率為0.32 ,所以成績在80.5~85.5分的學生頻率為0.16
所以成績在76.5~85.5分的學生頻率為0.26, ——2分
由于有900名學生參加了這次競賽,所以該校獲得二等獎的學生約為
0.26´900=234(人) ——2分


科目:高中數學 來源: 題型:
(本題滿分16分,第(1)小題6分,第(2)小題10分)
為了讓更多的人參與2010年在上海舉辦的“世博會”,上海某旅游公司面向國內外發行總量為2000萬張的旅游優惠卡,其中向境外人士發行的是世博金卡(簡稱金卡),向境內人士發行的是世博銀卡(簡稱銀卡)。現有一個由36名游客組成的旅游團到上海參觀旅游,其中![]() 是境外游客,其余是境內游客。在境外游客中有
是境外游客,其余是境內游客。在境外游客中有![]() 持金卡,在境內游客中有
持金卡,在境內游客中有![]() 持銀卡。.
持銀卡。. ![]()
![]()
![]()
(1)在該團中隨機采訪3名游客,求恰有1人持金卡且持銀卡者少于2人的概率;
(2)在該團的境內游客中隨機采訪3名游客,設其中持銀卡人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() 。
。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年黑龍江省高二上學期期末考試理科數學試卷(解析版) 題型:解答題
(本題12分)為了研究化肥對小麥產量的影響,某科學家將一片土地劃分成200個 的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
表1:施用新化肥小麥產量頻數分布表
|
小麥產量 |
|
|
|
|
|
|
頻數 |
10 |
35 |
40 |
10 |
5 |
表2:不施用新化肥小麥產量頻數分布表
|
小麥產量 |
|
|
|
|
|
頻數 |
15 |
50 |
30 |
5 |
(10) 完成下面頻率分布直方圖;

(2)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計施用化肥和不施用化肥的一小塊土地的小麥平均產量;
(3)完成下面2×2列聯表,并回答能否有99.5%的把握認為“施用新化肥和不施用新化肥的小麥產量有差異”
表3:
|
|
小麥產量小于20kg |
小麥產量不小于20kg |
合計 |
|
施用新化肥 |
|
|
|
|
不施用新化肥 |
|
|
|
|
合計 |
|
|
|
附:
|
|
0.050 |
0.010 |
0.005 |
0.001 |
|
|
3.841 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
科目:高中數學 來源:2010年上海市高二第二學期階段質量檢測數學試題 題型:解答題
(本題滿分16分,第(1)小題6分,第(2)小題10分)
如圖,彎曲的河流是近似的拋物線 ,公路
,公路 恰好是
恰好是 的準線,
的準線, 上的點
上的點 到
到 的距離最近,且為
的距離最近,且為 千米,城鎮
千米,城鎮 位于點
位于點 的北偏東
的北偏東 處,
處, 千米,現要在河岸邊的某處修建一座碼頭,并修建兩條公路,一條連接城鎮,一條垂直連接公路
千米,現要在河岸邊的某處修建一座碼頭,并修建兩條公路,一條連接城鎮,一條垂直連接公路 以便建立水陸交通網.
以便建立水陸交通網.
(1)建立適當的坐標系,求拋物線 的方程;
的方程;
(2)為了降低修路成本,必須使修建的兩條公路總長最小,請給出修建方案(作出圖形,在圖中標出此時碼頭 的位置),并求公路總長的最小值(精確到0.001千米)
的位置),并求公路總長的最小值(精確到0.001千米)

查看答案和解析>>
科目:高中數學 來源:2010年上海市高一上學期期中考試數學卷 題型:解答題
(本題滿分10分)甲乙兩地相距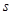 km,汽車從甲地勻速行駛到乙地,速度不得超過
km,汽車從甲地勻速行駛到乙地,速度不得超過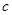 km/h,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度
km/h,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度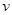 km/h的平方成正比,比例系數為
km/h的平方成正比,比例系數為 ,固定部分為
,固定部分為 元.
元.
(1)把全程運輸成本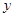 (元)表示為
(元)表示為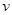 速度(千米/時)的函數,并指出這個函數的定義域;
速度(千米/時)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,汽車應以多大速度行駛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com