
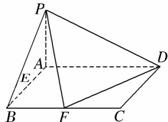
已知在四棱錐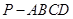 中,底面
中,底面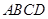 是矩形,且
是矩形,且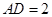 ,
,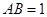 ,
, 平面
平面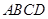 ,
,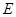 、
、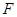 分別是線段
分別是線段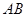 、
、 的中點.
的中點.
(1)證明: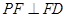 ;
;
(2)判斷并說明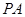 上是否存在點
上是否存在點 ,使得
,使得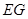 ∥平面
∥平面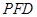 ;
;
(3)若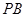 與平面
與平面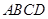 所成的角為
所成的角為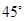 ,求二面角
,求二面角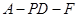 的余弦值.
的余弦值.
(1)見解析 (Ⅱ)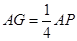 (Ⅲ)
(Ⅲ)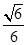 .
.
【解析】解法一(向量法)
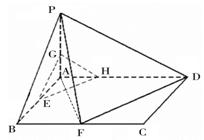
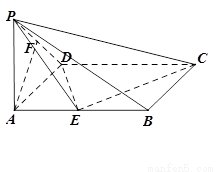
(I)建立如圖所示的空間直角坐標系A-xyz,分別求出直線PF與FD的平行向量,然后根據兩個向量的數量積為0,得到PF⊥FD;
(2)求出平面PFD的法向量(含參數t),及EG的方向向量,進而根據線面平行,則兩個垂直數量積為0,構造方程求出t值,得到G點位置;
(3)由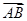 是平面PAD的法向量,根據PB與平面ABCD所成的角為45°,求出平面PFD的法向量,代入向量夾角公式,可得答案.
是平面PAD的法向量,根據PB與平面ABCD所成的角為45°,求出平面PFD的法向量,代入向量夾角公式,可得答案.
解法二(幾何法)
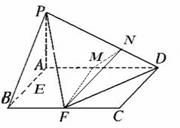
(I)連接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由線面垂直性質定理可得DF⊥PA,再由線面垂直的判定定理得到DF⊥平面PAF,再由線面垂直的性質定理得到PF⊥FD;
(Ⅱ)過點E作EH∥FD交AD于點H,則EH∥平面PFD,且有AH=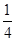 AD,再過點H作HG∥DP交PA于點G,則HG∥平面PFD且AG=
AD,再過點H作HG∥DP交PA于點G,則HG∥平面PFD且AG=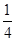 AP,由面面平行的判定定理可得平面GEH∥平面PFD,進而由面面平行的性質得到EG∥平面PFD.從而確定G點位置;
AP,由面面平行的判定定理可得平面GEH∥平面PFD,進而由面面平行的性質得到EG∥平面PFD.從而確定G點位置;
(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB與平面ABCD所成的角,即∠PBA=45°,取AD的中點M,則FM⊥AD,FM⊥平面PAD,在平面PAD中,過M作MN⊥PD于N,連接FN,則PD⊥平面FMN,則∠MNF即為二面角A-PD-F的平面角,解三角形MNF可得答案.
解法一:(Ⅰ)∵ 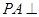 平面
平面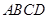 ,
,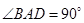 ,
,
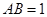 ,
, ,建立如圖所示的空間直角坐標系
,建立如圖所示的空間直角坐標系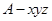 ,
,
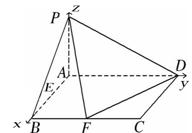
則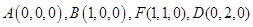 .…………2分
.…………2分
不妨令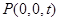 ∵
∵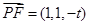 ,
,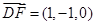
∴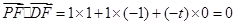 ,
,
即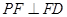 .…………………………4分
.…………………………4分
(Ⅱ)設平面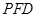 的法向量為
的法向量為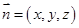 ,
,
由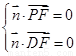 ,得
,得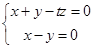 ,令
,令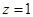 ,解得:
,解得: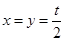 .∴
.∴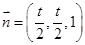 .
.
設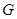 點坐標為
點坐標為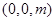 ,
,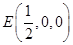 ,則
,則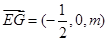 ,
,
要使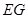 ∥平面
∥平面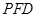 ,只需
,只需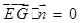 ,即
,即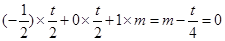 ,
,
得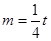 ,從而滿足
,從而滿足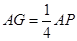 的點
的點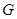 即為所求.………………8分
即為所求.………………8分
(Ⅲ)∵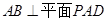 ,∴
,∴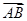 是平面
是平面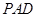 的法向量,易得
的法向量,易得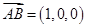 ,
,
又∵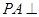 平面
平面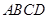 ,∴
,∴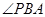 是
是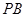 與平面
與平面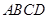 所成的角,
所成的角,
得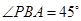 ,
,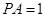 ,平面
,平面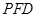 的法向量為
的法向量為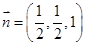 ……10分
……10分
∴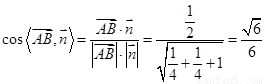 ,
,
故所求二面角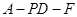 的余弦值為
的余弦值為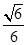 .………12分
.………12分
解法二:(Ⅰ)證明:連接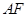 ,則
,則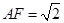 ,
,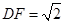 ,
,
又 ,∴
,∴
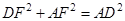 ,∴
,∴
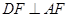 ……2分
……2分
又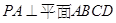 ,∴
,∴
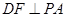 ,又
,又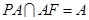 ,
,
∴ 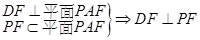 ……4分
……4分
(Ⅱ)過點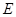 作
作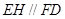 交
交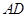 于點
于點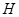 ,則
,則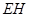 ∥平面
∥平面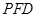 ,且有
,且有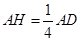 …5分
…5分
再過點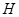 作
作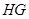 ∥
∥ 交
交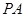 于點
于點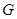 ,則
,則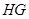 ∥平面
∥平面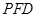 且
且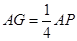 ,
,
∴ 平面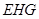 ∥平面
∥平面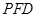 …………………7分∴
…………………7分∴
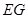 ∥平面
∥平面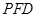 .
.
從而滿足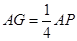 的點
的點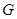 即為所求. …………………………8分
即為所求. …………………………8分
(Ⅲ)∵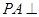 平面
平面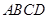 ,∴
,∴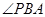 是
是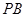 與平面
與平面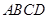 所成的角,且
所成的角,且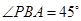 .
.
∴ 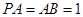 取
取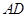 的中點
的中點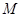 ,則
,則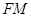
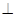
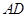 ,
,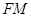
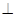 平面
平面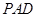 ,在平面
,在平面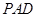 中,過
中,過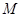 作
作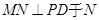 ,連接
,連接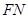 ,則
,則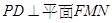 ,則
,則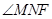 即為二面角
即為二面角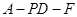 的平面角……10分
的平面角……10分
∵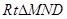 ∽
∽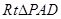 ,∴
,∴ 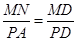 ,∵
,∵ ,且
,且 ∴
∴ 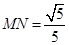 ,
,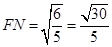 ,∴
,∴ 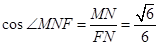


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:高中數學 來源:2015屆云南省高二上學期期中考試文科數學試卷(解析版) 題型:解答題
如圖,已知在四棱錐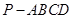 中,底面
中,底面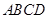 是矩形,
是矩形,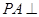 平面
平面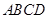 ,
,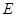 、
、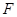 分別是
分別是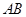 、
、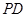 的中點.
的中點.
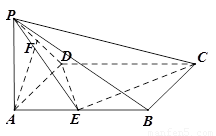
(Ⅰ)求證: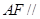 平面
平面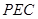 ;
;
(Ⅱ)若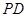 與平面
與平面 所成角為
所成角為 ,且
,且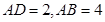 ,求點
,求點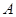 到平面
到平面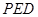 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源:2014屆河南省方城一高高三第一次調研(月考)考試理科數學試卷(解析版) 題型:解答題
已知在四棱錐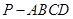 中,底面
中,底面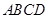 是矩形,
是矩形,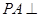 平面
平面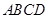 ,
,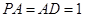 ,
,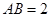 ,
,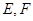 分別是
分別是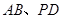 的中點.
的中點.
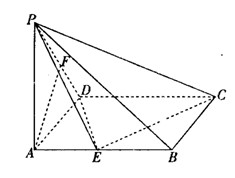
(1)求證: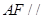 平面
平面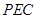 ;
;
(2)求二面角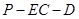 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年貴州省六高三第一次考理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)如圖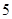 ,已知在四棱錐
,已知在四棱錐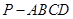 中,底面
中,底面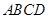 是矩形,
是矩形,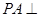 平面
平面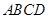 ,
,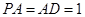 ,
,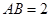 ,
,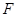 是
是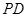 的中點,
的中點, 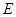 是線段
是線段 上的點.
上的點.
(I)當 是
是 的中點時,求證:
的中點時,求證: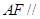 平面
平面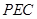 ;
;
(II)要使二面角 的大小為
的大小為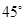 ,試確定
,試確定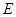 點的位置.
點的位置.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三下學期模擬沖刺考試理科數學試卷(解析版) 題型:解答題
(本小題滿分l2分)已知在四棱錐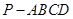 中,底面
中,底面 是矩形,且
是矩形,且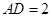 ,
, ,
,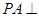 平面
平面 ,
,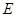 、
、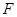 分別是線段
分別是線段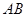 、
、 的中點.
的中點.
(1)證明: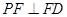 ;
;
(2)判斷并說明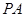 上是否存在點
上是否存在點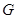 ,使得
,使得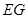 ∥平面
∥平面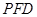 ;
;
(3)若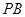 與平面
與平面 所成的角為
所成的角為 ,求二面角
,求二面角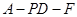 的余弦值.
的余弦值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com