
【題目】已知![]() ,
,
(1)求函數![]() 的單調區間;
的單調區間;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1) 函數在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減;(2)
上單調遞減;(2) ![]() .
.
【解析】試題分析:
(1)求出導數![]() ,在定義域內,解不等式
,在定義域內,解不等式![]() 得增區間,解不等式
得增區間,解不等式![]() 得減區間;(2)題設不等式可變形為
得減區間;(2)題設不等式可變形為![]() ,分別設
,分別設![]() ,
, ![]() ,求出它們的導數
,求出它們的導數![]() ,通過解相應不等式得出單調區間,求出最值,恰好是
,通過解相應不等式得出單調區間,求出最值,恰好是![]() 時,
時, ![]() 取最小值,
取最小值, ![]() 最最大值,因此要使原不等式恒成立,只要
最最大值,因此要使原不等式恒成立,只要![]() 即可.
即可.
試題解析:
(1)由![]() 得:
得: 
由于定義域為![]() ,
,
所以由![]() 得:
得: ![]()
所以由![]() 得:
得: ![]()
即得函數在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減。
上單調遞減。
(2)由不等式![]() 恒成立,
恒成立,
即![]() 恒成立
恒成立
設![]() 得:
得:
![]()
因為它們的定義域![]() ,所以易得:
,所以易得:
函數![]() 在
在![]() 上單調遞減,
上單調遞減, ![]() 上單調遞增;
上單調遞增;
函數![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() 上單調遞減;
上單調遞減;
這兩個函數在![]() 處,
處, ![]() 有最小值,
有最小值, ![]() 有最大值,
有最大值,
所以要使不等式![]() 恒成立,
恒成立,
則只需滿足![]() ,即
,即![]() .
.


 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的一段圖象如圖所示
)的一段圖象如圖所示 
(1)求f(x)的解析式;
(2)把f(x)的圖象向左至少平移多少個單位,才能使得到的圖象對應的函數為偶函數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中點,M是CE的中點,N點在PB上,且4PN=PB.
(Ⅰ)證明:平面PCE⊥平面PAB;
(Ⅱ)證明:MN∥平面PAC.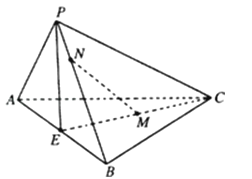
查看答案和解析>>
科目:高中數學 來源: 題型:
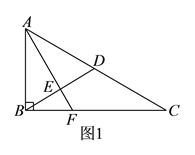
【題目】如圖![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 為
為![]() 中點,
中點, ![]() 于
于![]() (不同于點
(不同于點![]() ),延長
),延長![]() 交
交![]() 于
于![]() ,將
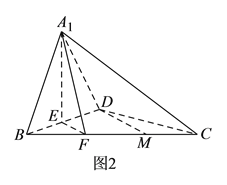
,將![]() 沿
沿![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,如圖
,如圖![]() 所示.
所示.
(Ⅰ)若![]() 是
是![]() 的中點,求證:直線
的中點,求證:直線![]() 平面
平面![]() .
.
(Ⅱ)求證: ![]() .
.
(Ⅲ)若平面![]() 平面
平面![]() ,試判斷直線
,試判斷直線![]() 與直線
與直線![]() 能否垂直?請說明理由.
能否垂直?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,側面
的正方形,側面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:面![]() 平面
平面![]() ;
;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某知名連鎖店分店開張營業期間,在固定的時間段內消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效展開,參與抽獎活動的人數越來越多,該分店經理對開業前7天參加抽獎活動的人數進行統計,![]() 表示開業第
表示開業第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:

經過進一步的統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)根據上表給出的數據,用最小二乘法,求出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該分店此次抽獎活動自開業始,持續10天,參加抽獎的每位顧客抽到一等獎(價值200元獎品)的概率為![]() ,抽到二等獎(價值100元獎品)的概率為
,抽到二等獎(價值100元獎品)的概率為![]() ,抽到三等獎(價值10元獎品)的概率為
,抽到三等獎(價值10元獎品)的概率為![]() ,試估計該分店在此次抽獎活動結束時送出多少元獎品?
,試估計該分店在此次抽獎活動結束時送出多少元獎品?
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,并在兩種坐標系中取相同的長度單位,已知直線
軸正半軸為極軸,并在兩種坐標系中取相同的長度單位,已知直線![]() 的參數方程為
的參數方程為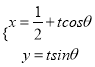 ,(
,( ![]() 為參數,
為參數, ![]() ),曲線
),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,當
兩點,當![]() 變化時,求
變化時,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com