
(07年湖北卷)(14分)
在平面直角坐標系![]() 中,過定點
中,過定點![]() 作直線與拋物線
作直線與拋物線![]() (
(![]() )相交于
)相交于![]() 兩點.
兩點.
(I)若點![]() 是點
是點![]() 關于坐標原點
關于坐標原點![]() 的對稱點,求
的對稱點,求![]() 面積的最小值;
面積的最小值;
(II)是否存在垂直于![]() 軸的直線
軸的直線![]() ,使得
,使得![]() 被以
被以![]() 為直徑的圓截得的弦長恒為定值?若存在,求出
為直徑的圓截得的弦長恒為定值?若存在,求出![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
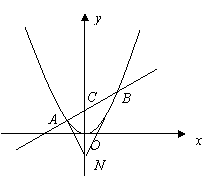
(此題不要求在答題卡上畫圖)
本小題主要考查直線、圓和拋物線等平面解析幾何的基礎知識,考查綜合運用數學知識進行推理運算的能力和解決問題的能力.
解析:解法1:(Ⅰ)依題意,點![]() 的坐標為
的坐標為![]() ,可設
,可設![]() ,
,
直線![]() 的方程為
的方程為![]() ,與
,與![]() 聯立得
聯立得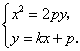 消去
消去![]() 得
得![]() .
.
由韋達定理得![]() ,
,![]() .
.
于是![]() .
.
![]()
![]() ,
,
![]() 當
當![]() ,
,![]() .
.
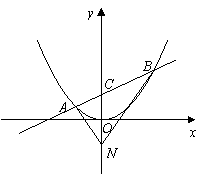
(Ⅱ)假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,
,
設![]() 的中點為
的中點為![]() ,
,![]() 與
與![]() 為直徑的圓相交于點
為直徑的圓相交于點![]() ,
,![]() 的中點為
的中點為![]() ,
,
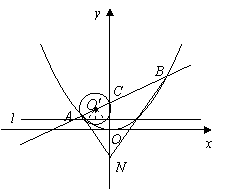
則![]() ,
,![]() 點的坐標為
點的坐標為![]() .
.
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() .
.
令![]() ,得
,得![]() ,此時
,此時![]() 為定值,故滿足條件的直線
為定值,故滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,
,
即拋物線的通徑所在的直線.
解法2:(Ⅰ)前同解法1,再由弦長公式得
![]()
![]() ,
,
又由點到直線的距離公式得![]() .
.
從而![]() ,
,
![]() 當
當![]() 時,
時,![]() .
.
(Ⅱ)假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,則以
,則以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() ,
,
將直線方程![]() 代入得
代入得![]() ,
,
則![]() .
.
設直線![]() 與以
與以![]() 為直徑的圓的交點為
為直徑的圓的交點為![]() ,
,
則有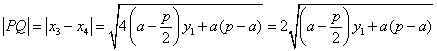 .
.
令![]() ,得
,得![]() ,此時
,此時![]() 為定值,故滿足條件的直線
為定值,故滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,
,
即拋物線的通徑所在的直線.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
(07年湖北卷理)平面![]() 外有兩條直線
外有兩條直線![]() 和
和![]() ,如果
,如果![]() 和
和![]() 在平面
在平面![]() 內的射影分別是
內的射影分別是![]() 和
和![]() ,給出下列四個命題:
,給出下列四個命題:
①![]() ;
;
②![]() ;
;
③![]() 與
與![]() 相交
相交![]()
![]() 與
與![]() 相交或重合;
相交或重合;
④![]() 與
與![]() 平行
平行![]()
![]() 與
與![]() 平行或重合.
平行或重合.
其中不正確的命題個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com