【題目】設數列{an}滿足a1+3a2+…+（2n﹣1）an=2n．（12分）
（1）求{an}的通項公式；
（2）求數列{ 
}的前n項和．
【答案】
（1）
解：數列{an}滿足a1+3a2+…+（2n﹣1）an=2n．
n≥2時，a1+3a2+…+（2n﹣3）an﹣1=2（n﹣1）．
∴（2n﹣1）an=2．∴an= 
．
當n=1時，a1=2，上式也成立．
∴an= ．
（2）
= 
= 
﹣ 
．
∴數列{ }的前n項和= 
+ 
. +…+ 
=1﹣ = 
．
【解析】（1）利用數列遞推關系即可得出．（2） = = ﹣ ．利用裂項相消求和方法即可得出．
【考點精析】認真審題，首先需要了解數列的前n項和(數列{an}的前n項和sn與通項an的關系
)，還要掌握數列的通項公式(如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式)的相關知識才是答題的關鍵．
舉一反三期末百分沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】隨著國家二孩政策的全面放開，為了調查一線城市和非一線城市的二孩生育意愿，某機構用簡單隨機抽樣方法從不同地區調查了100位育齡婦女，結果如下表.
非一線城市 | 一線城市 | 總計 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
總計 | 58 | 42 | 100 |
附表：
|
|
|
|
|
|
|
|
|
|
由
算得，
，
參照附表，得到的正確結論是
A. 在犯錯誤的概率不超過0.1%的前提下，認為“生育意愿與城市級別有關”
B. 在犯錯誤的概率不超過0.1%的前提下，認為“生育意愿與城市級別無關”
C. 有99%以上的把握認為“生育意愿與城市級別有關”
D. 有99%以上的把握認為“生育意愿與城市級別無關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，直線l1的參數方程為 
，（t為參數），直線l2的參數方程為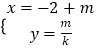 
，（m為參數）．設l1與l2的交點為P，當k變化時，P的軌跡為曲線C．
（Ⅰ）寫出C的普通方程；
（Ⅱ）以坐標原點為極點，x軸正半軸為極軸建立極坐標系，設l3：ρ（cosθ+sinθ）﹣ 
=0，M為l3與C的交點，求M的極徑．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等差數列{an}的公差d≠0滿足
成等比數列，若
=1，Sn是{
}的前n項和，則
的最小值為________．
【答案】4
【解析】
成等比數列，=1，可得：
= 
，即（1+2d）2=1+12d，d≠0，解得d．可得an，Sn．代入利用分離常數法化簡后，利用基本不等式求出式子的最小值．
∵成等比數列，a1=1，
∴= ，
∴（1+2d）2=1+12d，d≠0，
解得d=2．
∴an=1+2（n﹣1）=2n﹣1．
Sn=n+
×2=n2．
∴=
=n+1+
﹣2≥2
﹣2=4，
當且僅當n+1=時取等號，此時n=2，且取到最小值4，
故答案為：4．
【點睛】
本題考查了等差數列的通項公式、前n項和公式，等比中項的性質，基本不等式求最值，在利用基本不等式求最值時，要特別注意“拆、拼、湊”等技巧，使其滿足基本不等式中“正”(即條件要求中字母為正數)、“定”(不等式的另一邊必須為定值)、“等”(等號取得的條件)的條件才能應用，否則會出現錯誤.
【題型】填空題
【結束】
17
【題目】設
是公比為正數的等比數列,
,
(1)求的通項公式;
(2)設
是首項為1,公差為2的等差數列,求數列
的前
項和
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，曲線y=x2+mx﹣2與x軸交于A、B兩點，點C的坐標為（0，1），當m變化時，解答下列問題：（12分）
（1）能否出現AC⊥BC的情況？說明理由；
（2）證明過A、B、C三點的圓在y軸上截得的弦長為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在△ABC中，∠C=60°，D是BC上一點，AB=31，BD=20，AD=21．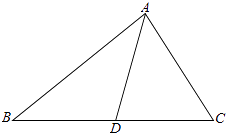 
（1）求cos∠B的值；
（2）求sin∠BAC的值和邊BC的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知直線l的參數方程為 
（t為參數，0＜α＜π），以原點O為極點，以x軸正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ= 
（p＞0）．
（Ⅰ）寫出直線l的極坐標方程和曲線C的直角坐標方程；
（Ⅱ）若直線l與曲線C相交于A，B兩點，求 
+ 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中點．
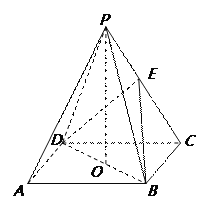
.求證：（Ⅰ）PA∥平面BDE；（Ⅱ）平面PAC⊥平面BDE；(III)若PB與底面所成的角為600, AB=2a,求三棱錐E-BCD的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于向量a,b,e及實數x,y,x1,x2,
，給出下列四個條件：
①
且
； ②
③
且唯一； ④
其中能使a與b共線的是 ( )
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
