
(本小題滿分15分)
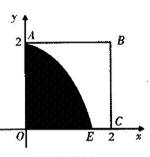
如圖,某小區(qū)有一邊長為2(單位:百米)的正方形地塊OABC,其中OAE是一個游泳池,計劃在地塊OABC內(nèi)修一條與池邊AE相切的直路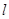 (寬度不計),切點為M,并把該地塊分為兩部分.現(xiàn)以點O為坐標(biāo)原點,以線段OC所在直線為x軸,建立平面直角坐標(biāo)系,若池邊AE滿足函數(shù)
(寬度不計),切點為M,并把該地塊分為兩部分.現(xiàn)以點O為坐標(biāo)原點,以線段OC所在直線為x軸,建立平面直角坐標(biāo)系,若池邊AE滿足函數(shù)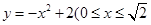 )的圖象,且點M到邊OA距離為
)的圖象,且點M到邊OA距離為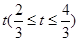 .
.
(1)當(dāng)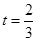 時,求直路
時,求直路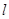 所在的直線方程;
所在的直線方程;
(2)當(dāng)t為何值時,地塊OABC在直路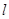 不含泳池那側(cè)的面積取到最大,最大值是多少?
不含泳池那側(cè)的面積取到最大,最大值是多少?
(1)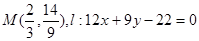 ;(2)
;(2)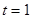 ,
,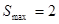 。
。
解析試題分析:(1)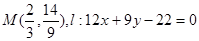
(2)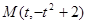 ,過切點M的切線
,過切點M的切線
即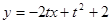 ,令
,令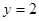 得
得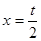 ,故切線
,故切線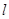 與AB交于點
與AB交于點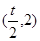 ;
;
令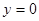 ,得
,得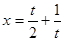 ,又
,又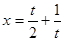 在
在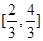 遞減,所以
遞減,所以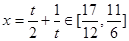
故切線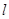 與OC交于點
與OC交于點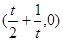 。
。 地塊OABC在切線
地塊OABC在切線 右上部分區(qū)域為直角梯形,
右上部分區(qū)域為直角梯形,
面積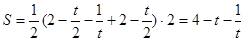
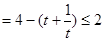 ,等號
,等號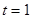 ,
,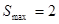 。
。
考點:本題主要考查函數(shù)模型,導(dǎo)數(shù)的幾何意義,導(dǎo)數(shù)的應(yīng)用,均值定理的應(yīng)用。
點評:中檔題,注意仔細(xì)審題。運用導(dǎo)數(shù)的幾何意義,求切線方程屬于簡單題,解題的關(guān)鍵是建立面積的表達(dá)式后,通過構(gòu)造,創(chuàng)造了應(yīng)用均值定理的條件,“一正、二定、三相等”。


科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù) 的定義域為
的定義域為 ,對任意的實數(shù)
,對任意的實數(shù) 都有
都有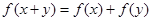 ;當(dāng)
;當(dāng) 時,
時, ,且
,且 .(1)判斷并證明
.(1)判斷并證明 在
在 上的單調(diào)性;
上的單調(diào)性;
(2)若數(shù)列 滿足:
滿足: ,且
,且 ,證明:對任意的
,證明:對任意的 ,
,
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)某企業(yè)擬投資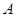 、
、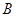 兩個項目,預(yù)計投資
兩個項目,預(yù)計投資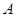 項目
項目 萬元可獲得利潤
萬元可獲得利潤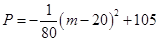
萬元;投資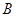 項目
項目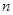 萬元可獲得利潤
萬元可獲得利潤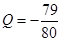
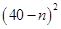
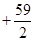
 萬元.若該企業(yè)用40
萬元.若該企業(yè)用40
萬元來投資這兩個項目,則分別投資多少萬元能獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)
(本小題滿分12分)某地方政府準(zhǔn)備在一塊面積足夠大的荒地上建一如圖所示的一個矩形綜合性休閑廣場,其總面積為3000平方米,其中場地四周(陰影部分)為通道,通道寬度均為2米,中間的三個矩形區(qū)域?qū)佋O(shè)塑膠地面作為運動場地(其中兩個小場地形狀相同),塑膠運動場地占地面積為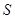 平方米.
平方米.
(1)分別寫出用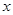 表示
表示 和用
和用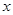 表示
表示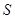 的函數(shù)關(guān)系式(寫出函數(shù)定義域);
的函數(shù)關(guān)系式(寫出函數(shù)定義域);
(2)怎樣設(shè)計能使S取得最大值,最大值為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)上海某玩具廠生產(chǎn) 套世博吉祥物“海寶”所需成本費用為
套世博吉祥物“海寶”所需成本費用為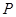 元,且
元,且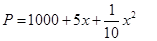 ,而每套“海寶”售出的價格為
,而每套“海寶”售出的價格為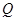 元,其中
元,其中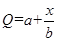
 ,
,
(1)問:該玩具廠生產(chǎn)多少套“海寶”時,使得每套所需成本費用最少?
(2)若生產(chǎn)出的“海寶”能全部售出,且當(dāng)產(chǎn)量為150套時利潤最大,此時每套價格為30元,求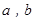 的值.(利潤 = 銷售收入-成本)
的值.(利潤 = 銷售收入-成本)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題共兩個小題,每題5分,滿分10分)
① 已知不等式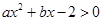 的解集是
的解集是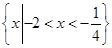 ,求
,求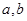 的值;
的值;
② 若函數(shù)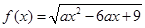 的定義域為
的定義域為 ,求實數(shù)
,求實數(shù)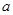 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com