
【題目】已知雙曲線![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,
, ![]() 是雙曲線C上的點(diǎn),
是雙曲線C上的點(diǎn), ![]() ,連接
,連接![]() 并延長
并延長![]() 交雙曲線C與點(diǎn)P,連接
交雙曲線C與點(diǎn)P,連接![]() ,若
,若![]() 是以
是以![]() 為頂點(diǎn)的等腰直角三角形,則雙曲線C的漸近線方程為( )
為頂點(diǎn)的等腰直角三角形,則雙曲線C的漸近線方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】如圖,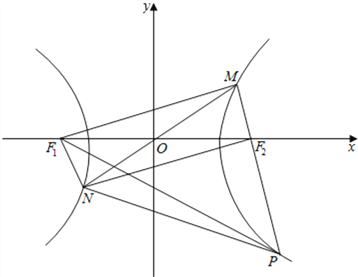
設(shè)F1為雙曲線左焦點(diǎn),連接MF1,NF1,則:
由對稱性可知四邊形F1NF2M
為平行四邊形;
又△NF2P是以∠NF2P為頂角的等腰直角三角形,
可得∠MF2N=90°;
∴F1NF2M為矩形;
設(shè)|MF2|=x,由雙曲線的定義可得,
|MF1|=2a+x;
∴|PF2|=|NF2|=|MF1|=2a+x;
∴|PF1|=2a+|PF2|=4a+x;
在Rt△MF1F2中有:
(2a+x)2+x2=4c2①;
在Rt△MF1P中有:(2a+x)2+(2a+2x)2=(4a+x)2②;
由②解得,x=a,代回①得:9a2+a2=4c2;
∴c2=![]() a2;∴b2=c2﹣a2=
a2;∴b2=c2﹣a2=![]() a2;
a2; ![]()
∴漸近線方程為:y=±![]() x=±
x=±![]() x.
x.
故答案為:B.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知:函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的極值;
的極值;
(2)若函數(shù)![]() ,討論
,討論![]() 的單調(diào)性;
的單調(diào)性;
(3)若函數(shù)![]() 的圖象與
的圖象與![]() 軸交于兩點(diǎn)
軸交于兩點(diǎn)![]() ,且
,且![]() .設(shè)
.設(shè)![]() ,其中常數(shù)
,其中常數(shù)![]() 、
、![]() 滿足條件
滿足條件![]() ,且
,且![]() .試判斷在點(diǎn)
.試判斷在點(diǎn)![]() 處的切線斜率的正負(fù),并說明理由.
處的切線斜率的正負(fù),并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓中心在坐標(biāo)原點(diǎn)O,焦點(diǎn)在![]() 軸上,長軸長是短軸長的2倍,且經(jīng)過點(diǎn)M(2,1),直線
軸上,長軸長是短軸長的2倍,且經(jīng)過點(diǎn)M(2,1),直線![]() 平行OM,且與橢圓交于A、B兩個不同的點(diǎn)。
平行OM,且與橢圓交于A、B兩個不同的點(diǎn)。
(Ⅰ)求橢圓方程;
(Ⅱ)若![]() AOB為鈍角,求直線
AOB為鈍角,求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 的取值范圍;
的取值范圍;
(Ⅲ)求證直線MA、MB與![]() 軸圍成的三角形總是等腰三角形。
軸圍成的三角形總是等腰三角形。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)記F(x)=f(x)﹣g(x),判斷F(x)在區(qū)間(1,2)內(nèi)零點(diǎn)個數(shù)并說明理由;
(Ⅱ)記(Ⅰ)中的F(x)在(1,2)內(nèi)的零點(diǎn)為x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有兩個不等實(shí)根x1 , x2(x1<x2),判斷x1+x2與2x0的大小,并給出對應(yīng)的證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】△ABC的三個內(nèi)角A、B、C的對邊分別是a、b、c,其面積S=a2﹣(b﹣c)2 . 若a=2,則BC邊上的中線長的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的側(cè)面PAD是正三角形,底面ABCD為菱形,A點(diǎn)E為AD的中點(diǎn),若BE=PE. 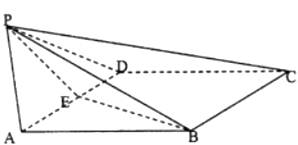
(1)求證:PB⊥BC;
(2)若∠PEB=120°,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com