
【題目】已知函數f(x)=ex(x2+ax-a),其中a是常數.
(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若存在實數k,使得關于x的方程f(x)=k在[0,+∞)上有兩個不相等的實數根,求k的取值范圍.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】
(1)求出![]() ,求出
,求出![]() 的值可得切點坐標,求出
的值可得切點坐標,求出![]() 的值,可得切線斜率,利用點斜式可得曲線
的值,可得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(Ⅱ)利用導數研究函數的單調性,可得函數
處的切線方程;(Ⅱ)利用導數研究函數的單調性,可得函數![]() 是
是![]() 上的減函數,是
上的減函數,是![]() 上的增函數,函數
上的增函數,函數![]() 在
在![]() 上的最小值為
上的最小值為![]() ., 且當
., 且當![]() 時,有
時,有![]()
![]() .,從而可求
.,從而可求![]() 的取值范圍.
的取值范圍.
(Ⅰ)由![]() 可得
可得
![]() .
.
當![]() 時,
時,![]() ,
,![]() .
.
所以 曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]() .
.
(Ⅱ) ![]() ,
,
解得![]() 或
或![]() .
.
當![]() ,即
,即![]() 時,在區間
時,在區間![]() 上,
上,![]() ,
,
所以![]() 是
是![]() 上的增函數.
上的增函數.
所以 方程![]() 在
在![]() 上不可能有兩個不相等的實數根.
上不可能有兩個不相等的實數根.
當![]() ,即
,即![]() 時,
時,![]() 隨
隨![]() 的變化情況如下表
的變化情況如下表
|
|
|
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
由上表可知函數![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
因為 函數![]() 是
是![]() 上的減函數,是
上的減函數,是![]() 上的增函數,
上的增函數,
且當![]() 時,有
時,有![]()
![]() .
.
所以 要使方程![]() 在
在![]() 上有兩個不相等的實數根,
上有兩個不相等的實數根,![]() 的取值范圍必須是
的取值范圍必須是
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
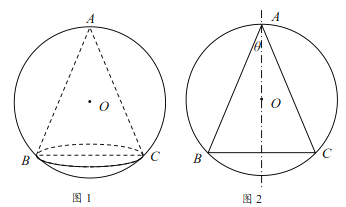
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓![]() 及其內接等腰三角形
及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉180°而成,如圖2.已知圓
旋轉180°而成,如圖2.已知圓![]() 的半徑為
的半徑為![]() ,設
,設![]() ,圓錐的側面積為
,圓錐的側面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積![]() 最大.求
最大.求![]() 取得最大值時腰
取得最大值時腰![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,長半軸長為短軸長的b倍,A,B分別為橢圓C的上、下頂點,點
,長半軸長為短軸長的b倍,A,B分別為橢圓C的上、下頂點,點![]() .
.
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 若直線MA,MB與橢圓C的另一交點分別為P,Q,證明:直線PQ過定點.
若直線MA,MB與橢圓C的另一交點分別為P,Q,證明:直線PQ過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空格內填入“充分非必要”或“必要非充分”或“充要”或“既非充分又非必要”.
(1)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(2)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(3)已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(4)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(5)“![]() ”是“AB”的________條件;
”是“AB”的________條件;
(6)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(7)“集合AB”是“![]() ”的________條件;
”的________條件;
(8)已知![]() ,“
,“![]() ”是“
”是“![]() ”的________條件.
”的________條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某物流公司欲將一批海產品從A地運往B地,現有汽車、火車、飛機三種運輸工具可供選擇,這三種工具的主要參考數據如下:
運輸工具 | 途中速度( | 途中費用(元/ | 裝卸時間( | 裝卸費用(元/ |
汽車 | 50 | 80 | 2 | 200 |
火車 | 100 | 40 | 3 | 400 |
飛機 | 200 | 200 | 3 | 800 |
若這批海產品在運輸過程中的損耗為300元/![]() ,問采用哪種運輸方式比較好,即運輸過程中的費用與損耗之和最小.
,問采用哪種運輸方式比較好,即運輸過程中的費用與損耗之和最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,兩焦點與短軸的一個頂點構成等腰直角三角形,且點
,兩焦點與短軸的一個頂點構成等腰直角三角形,且點 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖所示,過橢圓的左焦點作直線![]() (斜率存在且不為0)交橢圓
(斜率存在且不為0)交橢圓![]() 于
于![]() 兩點,過右焦點作直線
兩點,過右焦點作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,且
兩點,且![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,動點
,動點![]() (異于
(異于![]() )在橢圓上運動.
)在橢圓上運動.
①證明: ![]() 為常數;
為常數;
②當![]() 時,利用上述結論求
時,利用上述結論求![]() 面積的取值范圍.
面積的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一款擊鼓小游戲的規則如下:每輪游戲都需擊鼓三次,每次擊鼓要么出現一次音樂,要么不出現音樂;每輪游戲擊鼓三次后,出現一次音樂獲得10分,出現兩次音樂獲得20分,出現三次音樂獲得100分,沒有出現音樂則扣除200分(即獲得-200分).設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓是否出現音樂相互獨立.
,且各次擊鼓是否出現音樂相互獨立.
(1)玩三輪游戲,至少有一輪出現音樂的概率是多少?
(2)設每輪游戲獲得的分數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“大眾創業,萬眾創新”是李克強總理在本屆政府工作報告中向全國人民發出的口號.某生產企業積極響應號召,大力研發新產品,為了對新研發的一批產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到一組銷售數據![]() ,如表所示:
,如表所示:
試銷單價 | 4 | 5 | 6 | 7 | 8 | 9 |
產品銷量 |
| 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知變量![]() 具有線性相關關系,求產品銷量
具有線性相關關系,求產品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;可供選擇的數據:
;可供選擇的數據:![]() ,
,![]() ;
;
(3)用![]() 表示用(2)中所求的線性回歸方程得到的與
表示用(2)中所求的線性回歸方程得到的與![]() 對應的產品銷量的估計值.當銷售數據
對應的產品銷量的估計值.當銷售數據![]() 對應的殘差的絕對值
對應的殘差的絕對值![]() 時,則將銷售數據
時,則將銷售數據![]() 稱為一個“好數據”.現從6個銷售數據中任取3個,求“好數據”個數
稱為一個“好數據”.現從6個銷售數據中任取3個,求“好數據”個數![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
(參考公式:線性回歸方程中![]() 的最小二乘估計分別為
的最小二乘估計分別為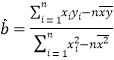 ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com