
【題目】設(shè)函數(shù)![]() ,若a是從1,2,3三個(gè)數(shù)中任取一個(gè),b是從2,3,4,5四個(gè)數(shù)中任取一個(gè),那么
,若a是從1,2,3三個(gè)數(shù)中任取一個(gè),b是從2,3,4,5四個(gè)數(shù)中任取一個(gè),那么![]() 恒成立的概率為( )
恒成立的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先把![]() 的解析式變形,用分離常數(shù)法,然后用均值不等式求出最小值,本題是一個(gè)古典概型,試驗(yàn)發(fā)生包含的所有事件是12個(gè),滿足條件的事件是10個(gè),即可得出答案.
的解析式變形,用分離常數(shù)法,然后用均值不等式求出最小值,本題是一個(gè)古典概型,試驗(yàn)發(fā)生包含的所有事件是12個(gè),滿足條件的事件是10個(gè),即可得出答案.
![]()
![]()
當(dāng)且僅當(dāng)![]() 時(shí),取“=”,
時(shí),取“=”,
∴![]() ,
,
于是![]() 恒成立就轉(zhuǎn)化為
恒成立就轉(zhuǎn)化為![]() 成立.
成立.
設(shè)事件A:“![]() 恒成立”,
恒成立”,
則基本事件總數(shù)為12個(gè),即
(1,2),(1,3),(1,4),(1,5);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5);
事件A包含事件:(1,2),(1,3);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5)共10個(gè)
所以![]() ,
,
故選:D


 孟建平名校考卷系列答案
孟建平名校考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知雙曲線![]() 的焦點(diǎn)是橢圓
的焦點(diǎn)是橢圓![]() :
: ![]() (
(![]() )的頂點(diǎn),且橢圓與雙曲線的離心率互為倒數(shù).
)的頂點(diǎn),且橢圓與雙曲線的離心率互為倒數(shù).
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)動(dòng)點(diǎn)![]() ,
, ![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,記直線
,記直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某多面體的三視圖如圖所示,則該多面體的各棱中,最長(zhǎng)棱的長(zhǎng)度為( )
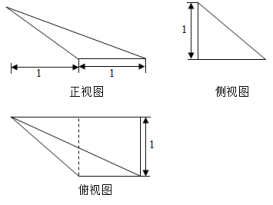
A. ![]() B.
B. ![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】推進(jìn)垃圾分類處理,是落實(shí)綠色發(fā)展理念的必然選擇,也是打贏污染防治攻堅(jiān)戰(zhàn)的重要環(huán)節(jié).為了解居民對(duì)垃圾分類的了解程度某社區(qū)居委會(huì)隨機(jī)抽取1000名社區(qū)居民參與問卷測(cè)試,并將問卷得分繪制頻率分布表如表:
得分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男性人數(shù) | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人數(shù) | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)從該社區(qū)隨機(jī)抽取一名居民參與問卷測(cè)試試估計(jì)其得分不低于60分的概率:
(2)將居民對(duì)垃圾分類的了解程度分為“比較了解”(得分不低于60分)和“不太了解”(得分低于60)兩類,完成2×2列聯(lián)表,并判斷是否有95%的把握認(rèn)為“居民對(duì)垃圾分類的了解程度”與“性別”有關(guān)?
不太了解 | 比較了解 | 合計(jì) | |
男性 | |||
女性 | |||
合計(jì) |
(3)從參與問卷測(cè)試且得分不低于80分的居民中,按照性別進(jìn)行分層抽樣,共抽取10人,現(xiàn)從這10人中隨機(jī)抽取3人作為環(huán)保宣傳隊(duì)長(zhǎng),設(shè)3人中男性隊(duì)長(zhǎng)的人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:![]() .
.
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若實(shí)數(shù)![]() 滿足
滿足![]() ,稱
,稱![]() 為函數(shù)
為函數(shù)![]() 的不動(dòng)點(diǎn).有下面三個(gè)命題:(1)若
的不動(dòng)點(diǎn).有下面三個(gè)命題:(1)若![]() 是二次函數(shù),且沒有不動(dòng)點(diǎn),則函數(shù)
是二次函數(shù),且沒有不動(dòng)點(diǎn),則函數(shù)![]() 也沒有不動(dòng)點(diǎn);(2)若
也沒有不動(dòng)點(diǎn);(2)若![]() 是二次函數(shù),則函數(shù)
是二次函數(shù),則函數(shù)![]() 可能有
可能有![]() 個(gè)不動(dòng)點(diǎn);(3)若
個(gè)不動(dòng)點(diǎn);(3)若![]() 的不動(dòng)點(diǎn)的個(gè)數(shù)是
的不動(dòng)點(diǎn)的個(gè)數(shù)是![]() ,則
,則![]() 的不動(dòng)點(diǎn)的個(gè)數(shù)不可能是
的不動(dòng)點(diǎn)的個(gè)數(shù)不可能是![]() ;它們中所有真命題的序號(hào)是________________________.
;它們中所有真命題的序號(hào)是________________________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的多面體ABCDE中,已知ABCD是邊長(zhǎng)為2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
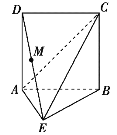
(1)若M是DE的中點(diǎn),試在AC上找一點(diǎn)N,使得MN∥平面ABE,并給出證明;
(2)求多面體ABCDE的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)定義在![]() 上的函數(shù)
上的函數(shù)![]() 和常數(shù)
和常數(shù)![]() ,
,![]() ,若
,若![]() 恒成立,則稱
恒成立,則稱![]() 為函數(shù)
為函數(shù)![]() 的一個(gè)“凱森數(shù)對(duì)”.
的一個(gè)“凱森數(shù)對(duì)”.
(1)若![]() 是
是![]() 的一個(gè)“凱森數(shù)對(duì)”,且
的一個(gè)“凱森數(shù)對(duì)”,且![]() ,求
,求![]() ;
;
(2)已知函數(shù)![]() 與
與![]() 的定義域都為
的定義域都為![]() ,問它們是否存在“凱森數(shù)對(duì)”?分別給出判斷并說(shuō)明理由;
,問它們是否存在“凱森數(shù)對(duì)”?分別給出判斷并說(shuō)明理由;
(3)若![]() 是
是![]() 的一個(gè)“凱森數(shù)對(duì)”,且當(dāng)
的一個(gè)“凱森數(shù)對(duì)”,且當(dāng)![]() 時(shí),
時(shí),![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的不動(dòng)點(diǎn)個(gè)數(shù)(函數(shù)
上的不動(dòng)點(diǎn)個(gè)數(shù)(函數(shù)![]() 的不動(dòng)點(diǎn)即為方程
的不動(dòng)點(diǎn)即為方程![]() 的解).
的解).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于函數(shù)![]() ,若存在區(qū)間
,若存在區(qū)間![]() ,使得
,使得![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“可等域函數(shù)”,區(qū)間A為函數(shù)的一個(gè)“可等域區(qū)間”.給出下列四個(gè)函數(shù):①
為“可等域函數(shù)”,區(qū)間A為函數(shù)的一個(gè)“可等域區(qū)間”.給出下列四個(gè)函數(shù):①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中存在唯一“可等域區(qū)間”的“可等域函數(shù)”的個(gè)數(shù)是( )
.其中存在唯一“可等域區(qū)間”的“可等域函數(shù)”的個(gè)數(shù)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市堅(jiān)持農(nóng)業(yè)與旅游融合發(fā)展,著力做好旅游各要素,完善旅游業(yè)態(tài),提升旅游接待能力.為了給游客提供更好的服務(wù),旅游部門需要了解游客人數(shù)的變化規(guī)律,收集并整理了![]() 年
年![]() 月至
月至![]() 年
年![]() 月期間月接待游客量(單位:萬(wàn)人)的數(shù)據(jù),繪制了如圖所示的折線圖.根據(jù)該折線圖,下列結(jié)論正確的是( )
月期間月接待游客量(單位:萬(wàn)人)的數(shù)據(jù),繪制了如圖所示的折線圖.根據(jù)該折線圖,下列結(jié)論正確的是( )
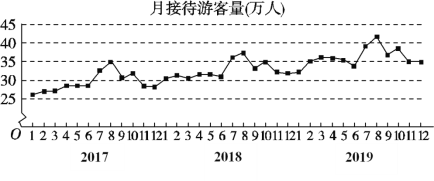
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對(duì)于7月至12月,波動(dòng)性更小,變化比較平穩(wěn)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com