
(1)求橢圓E的方程;
(2)若直線y=x與橢圓E交于M、N兩點(M點在第一象限),P、Q是橢圓上不同于M的相異兩點,點O為坐標原點,并且滿足(![]() +
+![]() )·(
)·(![]() -
-![]() )=0.試求直線PQ的斜率.
)=0.試求直線PQ的斜率.
解:(1)設橢圓的方程為![]() +
+![]() =1(a>b>0),
=1(a>b>0),
由題意,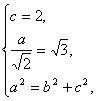 解得
解得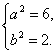 因此,橢圓的方程為
因此,橢圓的方程為![]() +
+![]() =1.
=1.
(2)由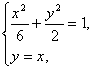 解之,得
解之,得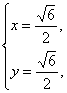 或
或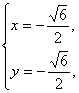
∴M(![]() ,
,![]() ).
).
∵(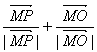 )·(
)·(![]() )=0,
)=0,
即(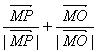 )·
)·![]() =0.
=0.
又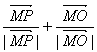 與∠PMQ的平分線共線,
與∠PMQ的平分線共線,
∴∠PMQ的平分線垂直于x軸.
若PM斜率存在,設PM的斜率為k,則QM的斜率為-k,
因此,PM和QM的方程分別為
y=k(x![]() )+
)+![]() ,y=-k(x
,y=-k(x![]() )+
)+![]() .由
.由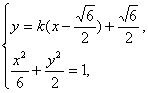
消去y并整理,得(1+3k2)x2-3![]() k(k-1)x+
k(k-1)x+![]() k2-9k
k2-9k![]() =0.(*)
=0.(*)
∵M(![]() ,
,![]() )在橢圓上,
)在橢圓上,
∴x=![]() 是方程(*)的一個根.
是方程(*)的一個根.
從而xP=![]() ,
,
同理xQ=![]() ,
,
從而直線PQ的斜率為
kPQ=![]() =
=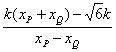 =
=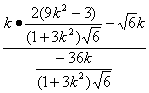 =
=![]() .
.
∴直線PQ的斜率為![]() .
.
若直線PM的斜率不存在,則點Q、M重合,與題設不符.
綜上所述,直線PQ的斜率為定值![]() .
.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
| y2 |
| 4 |
| AP |
| PB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com