
【題目】在某校舉行的航天知識競賽中,參與競賽的文科生與理科生人數之比為![]() ,且成績分布在
,且成績分布在![]() ,分數在
,分數在![]() 以上(含
以上(含![]() )的同學獲獎. 按文理科用分層抽樣的方法抽取
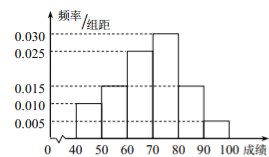
)的同學獲獎. 按文理科用分層抽樣的方法抽取![]() 人的成績作為樣本,得到成績的頻率分布直方圖(見下圖).
人的成績作為樣本,得到成績的頻率分布直方圖(見下圖).
(1)填寫下面的![]() 列聯表,能否有超過
列聯表,能否有超過![]() 的把握認為“獲獎與學生的文理科有關”?
的把握認為“獲獎與學生的文理科有關”?
(2)將上述調査所得的頻率視為概率,現從參賽學生中,任意抽取![]() 名學生,記“獲獎”學生人數為
名學生,記“獲獎”學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
文科生 | 理科生 | 合計 | |
獲獎 |
| ||
不獲獎 | |||
合計 |
|
附表及公式:
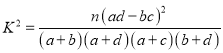 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)表見解析,有把握;(2)分布列見解析,![]() .
.
【解析】
試題分析:(1)首先根據頻率分布直方圖完成表格數據,然后根據公式計算出![]() ,再與臨界表比較,從而作出結論;(2)首先求得
,再與臨界表比較,從而作出結論;(2)首先求得![]() 的所有可能取值,然后分別求出相應概率,由此列出分布列,求得數學期望.
的所有可能取值,然后分別求出相應概率,由此列出分布列,求得數學期望.
試題解析:(1)
文科生 | 理科生 | 合計 | |
獲獎 | 5 | 35 | 40 |
不獲獎 | 45 | 115 | 160 |
合計 | 50 | 150 | 200 |
k==≈4.167>3.841,
所以有超過95%的把握認為“獲獎與學生的文理科有關”. …6分
(2)由表中數據可知,抽到獲獎同學的概率為,
將頻率視為概率,所以X可取0,1,2,3,且X~B(3,).
P(X=k)=C×()k(1-)3-k(k=0,1,2,3),
X | 0 | 1 | 2 | 3 |
P |
…10分
E(X)=3×=. …12分


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(
,( ![]() ,
, ![]() ).
).
(1)若![]() ,
, ![]() ,求函數
,求函數![]() 的單調增區間;
的單調增區間;
(2)若![]() 時,不等式
時,不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
, ![]() 時,記函數
時,記函數![]() 的導函數
的導函數![]() 的兩個零點是
的兩個零點是![]() 和
和![]() (
(![]() ),求證:
),求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以坐標原點為極點,以![]() 軸的非負半軸為極軸建立極坐標系,已知曲線
軸的非負半軸為極軸建立極坐標系,已知曲線![]() 的參數方程為
的參數方程為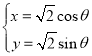 (
(![]() 為參數,
為參數,![]() ),直線
),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)點![]() 在曲線
在曲線![]() 上,且曲線
上,且曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求點
垂直,求點![]() 的極坐標;
的極坐標;
(2)設直線![]() 與曲線
與曲線![]() 有兩個不同的交點,求直線
有兩個不同的交點,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有兩枚均勻的硬幣和一枚不均勻的硬幣,其中不均勻的硬幣拋擲后出現正面的概率為![]() ,小華先拋擲這三枚硬幣,然后小紅再拋擲這三枚硬幣.
,小華先拋擲這三枚硬幣,然后小紅再拋擲這三枚硬幣.
(1)求小華拋得一個正面兩個反面且小紅拋得兩個正面一個反面的概率;
(2)若用![]() 表示小華拋得正面的個數,求
表示小華拋得正面的個數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來蓬勃發展的新機遇,2016年雙11期間,某平臺的銷售業績高達918億人民幣,與此同時,相關管理部門也推出了針對電商的商品和服務評價體系,現從評價系統中隨機選出200次成功的交易,并對其評價結果進行統計,對商品的好評率為![]() ,對服務的好評率為
,對服務的好評率為![]() ,其中對商品和服務都做出好評的交易為80次.
,其中對商品和服務都做出好評的交易為80次.
在犯錯誤概率不超過( )的前提下,認為商品好評與服務好評有關.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數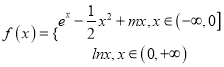 ,
, ![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)若函數![]() 的圖象在
的圖象在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 時,函數
時,函數![]() 在
在![]() 內是增函數,求
內是增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設函數
時,設函數![]() 的圖象
的圖象![]() 與函數
與函數![]() 的圖象
的圖象![]() 交于點
交于點![]() 、
、![]() ,過線段
,過線段![]() 的中點
的中點![]() 作
作![]() 軸的垂線分別交
軸的垂線分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,問是否存在點
,問是否存在點![]() ,使
,使![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線平行?若存在,求出
處的切線平行?若存在,求出![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系下,曲線
軸的正半軸為極軸的極坐標系下,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 和曲線
和曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com