
如圖,過拋物線y2=2PX(P>0)的焦點F的直線與拋物線相交于M、N兩點,自M、N向準線L作垂線,垂足分別為M1、N1
 (Ⅰ)求證:FM1⊥FN1:
(Ⅰ)求證:FM1⊥FN1:
(Ⅱ)記△FMM1、、△FM1N1、△FN N1的面積分別為S1、、S2、,S3,試判斷S22=4S1S3是否成立,并證明你的結論。 ![]()
本小題主要考查拋物線的概念,拋物線的幾何性質等平面解析幾何的基礎知識,考查綜合運用數學知識進行推理運算的能力(滿分13分)
(1) 證法1:由拋物線的定義得
![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() 2分
2分
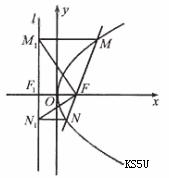 如圖,設準線l與x的交點為
如圖,設準線l與x的交點為![]()
![]()
![]()
而![]()
即![]()
![]()
故![]()
證法2:依題意,焦點為![]() 準線l的方程為
準線l的方程為![]()
設點M,N的坐標分別為![]() 直線MN的方程為
直線MN的方程為![]() ,則有
,則有
![]()
由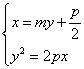 得
得![]()
于是,![]() ,
,![]()
![]() ,故
,故![]()
(Ⅱ)![]() 成立,證明如下:
成立,證明如下:
證法1:設![]() ,則由拋物線的定義得
,則由拋物線的定義得
![]() ,于是
,于是
![]()
![]()
![]()
![]()
![]()
將 與
與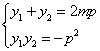 代入上式化簡可得w.w.w.k.s.5.u.c.o.m
代入上式化簡可得w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ,此式恒成立。
,此式恒成立。
故![]() 成立。
成立。
證法2:如圖,設直線![]() M的傾角為
M的傾角為![]() ,
,![]()
則由拋物線的定義得![]()
![]()
于是![]()
在![]() 和
和![]() 中,由余弦定理可得
中,由余弦定理可得
![]()
由(I)的結論,得![]()
![]()
即![]() ,得證。
,得證。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
如圖,過拋物線y2=2PX(P>0)的焦點F的直線與拋物線相交于M、N兩點,自M、N向準線L作垂線,垂足分別為M1、N1

(Ⅰ)求證:FM1⊥FN1:
(Ⅱ)記△FMM1、、△FM1N1、△FN N1的面積分別為![]() ,試判斷S22=4S1S3是否成立,并證明你的結論。w.w.w.k.s.5.u.c.o.m
,試判斷S22=4S1S3是否成立,并證明你的結論。w.w.w.k.s.5.u.c.o.m ![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,過拋物線y2=2PX(P>0)的焦點F的直線與拋物線相交于M、N兩點,自M、N向準線L作垂線,垂足分別為M1、N1

(Ⅰ)求證:FM1⊥FN1:
(Ⅱ)記△FMM1、、△FM1N1、△FN N1的面積分別為S1、、S2、,S3,試判斷S22=4S1S3是否成立,并證明你的結論。w.w.w.k.s.5.u.c.o.m ![]()
![]()
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南省鎮平一高高三下學期第四次周考文科數學試卷 題型:選擇題
如圖,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A、B,交其準線于點C,若|BC|=2|BF|,且|AF|=3,則此拋物線的方程為
A.y2=9x B.y2=6x
C.y2=3x D.y2= x
x
查看答案和解析>>
科目:高中數學 來源:2010年浙江省杭州市七校聯考高二下學期期中考試數學(理) 題型:選擇題
如圖,過拋物線y2=2px(p>0)的焦點F的直線 交拋物線
交拋物線
于點A、B,交其準線于點C,若|BC|=2|BF|,且|AF|=3,
則此拋物線的方程為 ( )

A.y2=3x B.y2=6x C.y2=9x D.y2=
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com