【題目】已知函數
，
，
.
（1）求
的最大值；
（2）若對
，總存在
，使得
成立，求
的取值范圍.
【答案】（1）
；（2）
.
【解析】
（1）利用導數分析函數
的單調性，進而可求得函數的最大值；
（2）由題意可知
，對函數
求導，對實數
的取值進行分類討論，利用導數分析函數在區間
上的單調性，結合
可得出關于實數的不等式，進而可求得實數的取值范圍.
（1）函數
的定義域為
，
，
當
時，
；當
時，
.
所以，函數的單調遞增區間為
，單調遞減區間為
，
所以，函數在
處取得極大值，亦即最大值，即
；
（2）由題意可知，即.
，則
，所以，函數
在區間上單調遞增，
當
時，
，即
.
①當
時，即當
時，
對任意的恒成立，
此時，函數在區間上單調遞增，則
，
，解得
，此時；
②當
時，即當
時，
對任意的恒成立，
此時，函數在區間上單調遞減，則
，
，解得
，此時
；
③當
時，即當
時，則存在
，使得
，
且當
時，
；當
時，
.
所以，函數在區間
上單調遞減，在區間
上單調遞增，
，
，
.
當
時，
，解得
；
當
時，
，解得，此時.
綜上所述，實數的取值范圍是.
科目：高中數學 來源： 題型：
【題目】已知在等比數列{an}中，
＝2，，
＝128，數列{bn}滿足b1＝1，b2＝2，且{
}為等差數列．
（1）求數列{an}和{bn}的通項公式；
（2）求數列{bn}的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠連續6天對新研發的產品按事先擬定的價格進行試銷，得到一組數據
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
試銷價 | 9 | 11 | 10 | 12 | 13 | 14 |
產品銷量 | 40 | 32 | 29 | 35 | 44 |
|
（1）試根據4月2日、3日、4日的三組數據，求
關于
的線性回歸方程
，并預測4月6日的產品銷售量
；
（2）若選取兩組數據確定回歸方程，求選取得兩組數據恰好是不相鄰兩天的事件
的概率.
參考公式：
其中
，
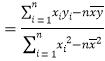查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高血壓高血糖和高血脂統稱“三高”.如圖是西南某地區從2010年至2016年患“三高”人數y(單位：千人)的折線圖.
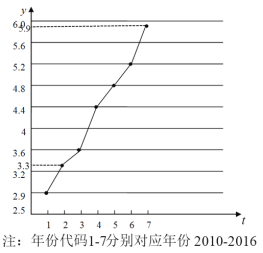
（1）由折線圖看出，可用線性回歸模型擬合
與
的關系，請求出相關系數(精確到0.01)并加以說明；
（2）建立關于的回歸方程，預測2018年該地區患“三高”的人數.
參考數據：
，
，
，
.
參考公式：相關系數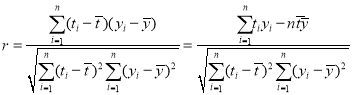
，
回歸方程
中：
，
.
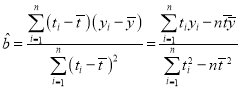查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一種特別列車，沿途共有
個車站（包括起點與終點），因安全需要，規定在同一車站上車的旅客不能在同一車站下車。為了保證上車的旅客都有座位（每位旅客一個座位），則列車至少要安排（）個座位。
A. 
B. 100 C. 110 D. 120
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】共享單車的投放，方便了市民短途出行，被譽為中國“新四大發明”之一.某市為研究單車用戶與年齡的相關程度，隨機調查了100位成人市民，統計數據如下：
不小于40歲 | 小于40歲 | 合計 | |
單車用戶 | 12 | y | m |
非單車用戶 | x | 32 | 70 |
合計 | n | 50 | 100 |
（1）求出列聯表中字母x、y、m、n的值；
（2）①從此樣本中，對單車用戶按年齡采取分層抽樣的方法抽出5人進行深入調研，其中不小于40歲的人應抽多少人？
②從獨立性檢驗角度分析，能否有
以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關.
下面臨界值表供參考：
P（ | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
