
【題目】某高科技企業研制出一種型號為A的精密數控車床,A型車床為企業創造的價值逐年減少(以投產一年的年初到下一年的年初為A型車床所創造價值的第一年).若第 1 年A型車床創造的價值是250萬元,且第1年至第6年,每年A型車床創造的價值減少30萬元;從第7年開始,每年A型車床創造的價值是上一年價值的 50%.現用![]() (
(![]() )表示A型車床在第n年創造的價值.
)表示A型車床在第n年創造的價值.
(1)求數列![]() 的通項公式
的通項公式![]() ;
;
(2)記![]() 為數列
為數列![]() 的前n項的和
的前n項的和![]()
![]() ,企業經過成本核算,若
,企業經過成本核算,若![]() 萬元,則繼續使用A型車床,否則更換A型車床,試問該企業須在第幾年年初更換A型車床?(已知:若正數數列
萬元,則繼續使用A型車床,否則更換A型車床,試問該企業須在第幾年年初更換A型車床?(已知:若正數數列![]() 是單調遞減數列,則數列
是單調遞減數列,則數列![]() 也是單調遞減數列).
也是單調遞減數列).
【答案】(1)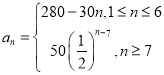 (
(![]() );(2)12
);(2)12
【解析】
(1)由題意可得:第1年至第6年時為遞減等差數列,易求![]() ;從第7年開始為以
;從第7年開始為以![]() 為首項,公比
為首項,公比![]() 的等比數列,則可求得
的等比數列,則可求得![]() ;
;
(2)由(1)知數列![]() 是單調遞減數列,則
是單調遞減數列,則![]() 也是單調遞減數列,當
也是單調遞減數列,當![]() 時,易求
時,易求![]() 100萬元;當
100萬元;當![]() 時,通過計算判斷
時,通過計算判斷![]() 萬元,
萬元,![]() 萬元,則可得第12年年初更換車床.
萬元,則可得第12年年初更換車床.
(1)由題意可得在第1年至第6年時數列![]() 為以
為以![]() 為首項,公差
為首項,公差![]() 的等差數列,所以可得
的等差數列,所以可得![]() 在第7年開始數列
在第7年開始數列![]() 是以
是以![]() 為首項,公比
為首項,公比![]() 的等比數列,則可求得
的等比數列,則可求得![]() ,
,
綜上可得數列![]() 的通項公式
的通項公式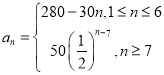 (
(![]() );
);
(2)由(1)知數列![]() 是單調遞減數列,則由題意得新數列
是單調遞減數列,則由題意得新數列![]() 即
即![]() 也是單調遞減數列,當
也是單調遞減數列,當![]() 時,
時,![]() (萬元),所以前六年不用更換車床;
(萬元),所以前六年不用更換車床;
當![]() 時,
時,
由![]() (萬元),
(萬元),![]() (萬元),且
(萬元),且![]() 是單調遞減數列,可得當
是單調遞減數列,可得當![]() 時,
時,![]() (萬元)恒成立,所以該企業必須在第12年年初更換車床.
(萬元)恒成立,所以該企業必須在第12年年初更換車床.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左.右焦點分別為
的左.右焦點分別為![]() ,短軸兩個端點為
,短軸兩個端點為![]() ,且四邊形
,且四邊形![]() 的邊長為
的邊長為![]() 的正方形.
的正方形.
(Ⅰ)求橢圓的方程;
(Ⅱ)若![]() ,分別是橢圓長軸的左,右端點,動點
,分別是橢圓長軸的左,右端點,動點![]() 滿足
滿足![]() ,連結
,連結![]() ,交橢圓于點
,交橢圓于點![]() .證明:
.證明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的條件下,試問![]() 軸上是否存在異于點
軸上是否存在異于點![]() ,的定點
,的定點![]() ,使得以
,使得以![]() 為直徑的圓恒過直線
為直徑的圓恒過直線![]() ,
,![]() 的交點,若存在,求出點
的交點,若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某地區2012年至2018年生活垃圾無害化處理量(單位:萬噸)的折線圖.
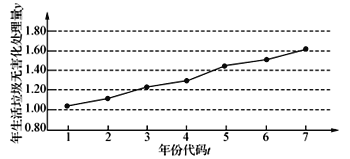
注:年份代碼![]() 分別表示對應年份
分別表示對應年份![]() .
.
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數
的關系,請用相關系數![]() (
(![]() 線性相關較強)加以說明;
線性相關較強)加以說明;
(2)建立![]() 與
與![]() 的回歸方程(系數精確到0.01),預測2019年該區生活垃圾無害化處理量.
的回歸方程(系數精確到0.01),預測2019年該區生活垃圾無害化處理量.
(參考數據)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(參考公式)相關系數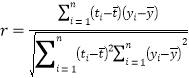 ,在回歸方程
,在回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: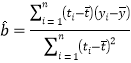 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為雙曲線
為雙曲線![]() :
: ![]() 的左、右焦點,過
的左、右焦點,過![]() 作垂直于
作垂直于![]() 軸的直線,在
軸的直線,在![]() 軸上方交雙曲線C于點
軸上方交雙曲線C于點![]() ,且
,且![]()
(1)求雙曲線C的方程;
(2)若直線![]() 與雙曲線C恒有兩個不同交點P和Q且
與雙曲線C恒有兩個不同交點P和Q且![]() (其中O為原點),求k的取值范圍;
(其中O為原點),求k的取值范圍;
(3)過雙曲線C上任意一點R作該雙曲線兩條漸近線的垂線,垂足分別為M,N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中有如下正確結論:
中有如下正確結論:![]() 為曲線
為曲線![]() (
(![]() 、
、![]() 為非零實數,且不同時為負)上一點,則過點
為非零實數,且不同時為負)上一點,則過點![]() 的切線方程為
的切線方程為![]() .
.
(1)已知![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為過點
為過點![]() 的橢圓的切線,若直線
的橢圓的切線,若直線![]() 與直線
與直線![]() 的斜率分別為
的斜率分別為![]() 與
與![]() ,求證:
,求證:![]() 為定值;
為定值;
(2)過橢圓![]() 上一點
上一點![]() 引橢圓
引橢圓![]() 的切線,與
的切線,與![]() 軸交于點
軸交于點![]() .若
.若![]() 為正三角形,求橢圓
為正三角形,求橢圓![]() 的方程;
的方程;
(3)求與圓![]() 及(2)中的橢圓
及(2)中的橢圓![]() 均相切的直線
均相切的直線![]() 與坐標軸圍成的三角形的面積的取值范圍.
與坐標軸圍成的三角形的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題![]() :方程
:方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線:命題
軸上的雙曲線:命題![]() :若存在
:若存在![]() ,使得
,使得![]() 成立.
成立.
(1)如果命題![]() 是真命題,求實數
是真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)如果“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點![]() 的動直線
的動直線![]() 與圓
與圓![]() :
:![]() 相交于
相交于![]() 、
、![]() 兩點,
兩點,![]() 是
是![]() 中點,
中點,![]() 與直線
與直線![]() :
:![]() (
(![]() 為常數)相交于點
為常數)相交于點![]() .
.
(1)求證:當![]() 與
與![]() 垂直時,
垂直時,![]() 必過圓心
必過圓心![]() ;
;
(2)當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(3)當直線![]() 的傾斜角
的傾斜角![]() 變化時,探索
變化時,探索![]() 的值是否為常數?若是,求出該常數;若不是,請說明理由.
的值是否為常數?若是,求出該常數;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點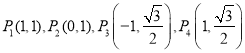 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求橢圓C的方程
(2)橢圓C上是否存在不同的兩點M,N關于直線![]() 對稱?若存在,請求出直線MN的方程,若不存在,請說明理由.
對稱?若存在,請求出直線MN的方程,若不存在,請說明理由.
(3)設直線l不經過點![]() 且與C相交于A,B兩點,若直線
且與C相交于A,B兩點,若直線![]() 與直線
與直線![]() 的斜率之和為1,求證直線l必過定點,并求出這個定點坐標.
的斜率之和為1,求證直線l必過定點,并求出這個定點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com