
【題目】我國加入WTO時,根據(jù)達成的協(xié)議,某產(chǎn)品的市場供應(yīng)量P與市場價格x的關(guān)系近似滿足P(x)=2(1-kt)(x-b)2(其中t為關(guān)銳的稅率,且t∈[0, ![]() ),x為市場價格,b、k為正常數(shù)).當(dāng)t=
),x為市場價格,b、k為正常數(shù)).當(dāng)t=![]() 時的市場供應(yīng)量曲線如圖所示.
時的市場供應(yīng)量曲線如圖所示.

(1)根據(jù)圖象求b、k的值;
(2)記市場需求量為Q,它近似滿足Q(x)=![]() ,當(dāng)P=Q時的市場價格稱為市場平衡價格,為使市場平衡價格不低于9元,求稅率的最小值.
,當(dāng)P=Q時的市場價格稱為市場平衡價格,為使市場平衡價格不低于9元,求稅率的最小值.
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題:
①若![]() ,則
,則![]() ;
;
②已知![]() ,
,![]() ,且
,且![]() 與
與![]() 的夾角為銳角,則實數(shù)
的夾角為銳角,則實數(shù)![]() 的取值范圍是
的取值范圍是![]() ;
;
③已知![]() 是平面上一定點,
是平面上一定點,![]() 是平面上不共線的三個點,動點
是平面上不共線的三個點,動點![]() 滿足
滿足![]() ,
,![]() ,則
,則![]() 的軌跡一定通過
的軌跡一定通過![]() 的重心;
的重心;
④在![]() 中,
中,![]() ,邊長
,邊長![]() 分別為
分別為![]() ,則
,則![]() 只有一解;
只有一解;
⑤如果△ABC內(nèi)接于半徑為![]() 的圓,且
的圓,且![]()
則△ABC的面積的最大值![]() ;
;
其中正確的序號為_______________________。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 有是實數(shù)解時,求實數(shù)
有是實數(shù)解時,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,對一切
,對一切![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量a=![]() cosωx+1,2sinωx,b=
cosωx+1,2sinωx,b=![]() cosωx-
cosωx-![]() ,cosωx), ω>0.
,cosωx), ω>0.
(Ⅰ)當(dāng)ωx≠kπ+![]() ,k∈Z時,若向量c=(1,0),d=(
,k∈Z時,若向量c=(1,0),d=(![]() ,0),且(a-c)∥(b+d),求4sin2ωx-cos2ωx的值;
,0),且(a-c)∥(b+d),求4sin2ωx-cos2ωx的值;
(Ⅱ)若函數(shù)f(x)=a·b的圖象的相鄰兩對稱軸之間的距離為![]() ,當(dāng)x∈[
,當(dāng)x∈[![]() ],g時,求函數(shù)f(x)的單調(diào)遞增區(qū)間.
],g時,求函數(shù)f(x)的單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x2+alnx(a為實常數(shù))
(Ⅰ)若a=﹣2,求證:函數(shù)f(x)在(1,+∞)上是增函數(shù);
(Ⅱ)求函數(shù)f(x)在[1,e]上的最小值及相應(yīng)的x值;
(Ⅲ)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() ,
,  ,
, 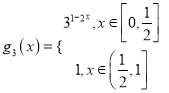 ,
, ![]() 在等差數(shù)列
在等差數(shù)列![]() 中,
中, ![]() ,
,
用![]() 表示數(shù)列
表示數(shù)列![]() 的前2018項的和,則( )
的前2018項的和,則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某幼兒園為訓(xùn)練孩子的數(shù)字運算能力,在一個盒子里裝有標號為1,2,3,4,5的卡片各兩張,讓孩子從盒子里任取3張卡片,按卡片上的最大數(shù)字的9倍計分,每張卡片被取出的可能性都相等,用X表示取出的3張卡片上的最大數(shù)字
(1)求取出的3張卡片上的數(shù)字互不相同的概率;
(2)求隨機變量X的分布列及數(shù)學(xué)期望;
(3)若孩子取出的卡片的計分超過30分,就得到獎勵,求孩子得到獎勵的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x+2a|+|x﹣1|,a∈R.
(1)當(dāng)a=1時,解不等式f(x)≤5;
(2)若f(x)≥2對于x∈R恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象與
的圖象與![]() 軸的交點中相鄰兩個交點的距離是
軸的交點中相鄰兩個交點的距離是![]() ,當(dāng)
,當(dāng)![]() 時
時![]() 取得最小值
取得最小值![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 的最大值和最小值;
的最大值和最小值;
(3)若函數(shù)![]() 的零點為
的零點為![]() ,求
,求![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com