已知橢圓
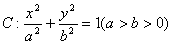
的左頂點
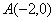
,過右焦點
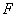
且垂直于長軸的弦長為
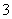
.
(Ⅰ)求橢圓
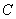
的方程;
(Ⅱ)若過點
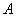
的直線
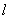
與橢圓交于點
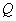
,與
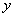
軸交于點
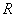
,過原點與
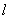
平行的直線與橢圓交于點

,求證:
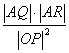
為定值.
(1)
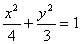
(2)
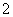
試題分析:解:(1)
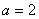
,設(shè)過右焦點
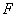
且垂直于長軸的弦為
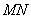
,將
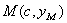
代入橢圓方程
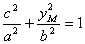
,解得
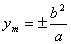
, 2分
故
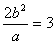
,可得
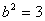
. 4分
所以,橢圓方程為
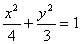
. 6分
(2)由題意知,直線
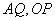
斜率存在,故設(shè)為
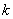
,則直線
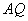
的方程為
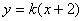
,直線
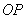
的方程為
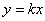
.可得
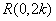
,則
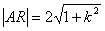
. 8分
設(shè)
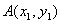
,
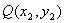
,聯(lián)立方程組
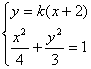
,
消去
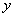
得:

,
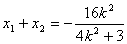
,

,
則
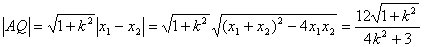
. 11分
設(shè)
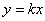
與橢圓交另一點為
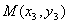
,
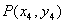
,聯(lián)立方程組
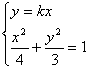
,
消去
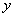
得
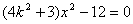
,
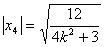
,
所以
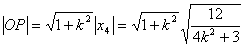
. 13分
故
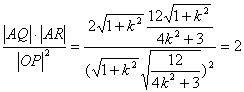
.
所以
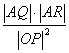
等于定值
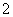
. 15分
點評:本題主要考橢圓的幾何性質(zhì),直線與橢圓的位置關(guān)系等基礎(chǔ)知識,考查解析幾何的基本思想方法和綜合解題能力
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
焦點在x軸上的橢圓
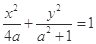
的離心率的最大值為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在平面斜坐標系
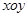
中
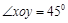
,點
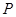
的斜坐標定義為:“若
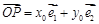
(其中
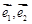
分別為與斜坐標系的
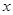
軸,
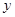
軸同方向的單位向量),則點
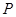
的坐標為
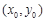
”.若
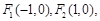
且動點
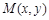
滿足
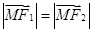
,則點
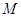
在斜坐標系中的軌跡方程為
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若拋物線
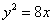
的焦點與雙曲線
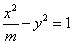
的右焦點重合,則雙曲線的離心率為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知橢圓C的對稱中心為原點O,焦點在x軸上,左右焦點分別為
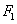
和
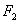
,且|
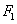
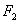
|=2,
點(1,
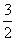
)在該橢圓上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過
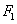
的直線
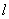
與橢圓C相交于A,B兩點,若

A
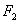
B的面積為
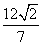
,求以
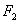
為圓心且與直線
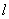
相切是圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知雙曲線
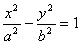
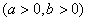
的漸近線與圓
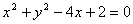
有公共點,則該雙曲線的離心率的取值范圍是___________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
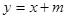
與拋物線
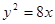
交于A、B兩點,
(1)若|AB|="10," 求實數(shù)
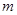
的值。
(2)若
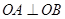
, 求實數(shù)
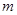
的值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知橢圓
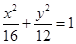
,則以點
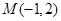
為中點的弦所在直線方程為__________________。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若方程
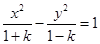
表示雙曲線,則實數(shù)
k的取值范圍是 ( )
查看答案和解析>>

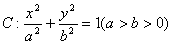 的左頂點
的左頂點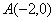 ,過右焦點
,過右焦點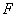 且垂直于長軸的弦長為
且垂直于長軸的弦長為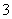 .
.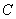 的方程;
的方程;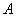 的直線
的直線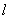 與橢圓交于點
與橢圓交于點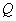 ,與
,與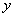 軸交于點
軸交于點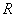 ,過原點與
,過原點與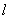 平行的直線與橢圓交于點
平行的直線與橢圓交于點 ,求證:
,求證: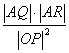 為定值.
為定值.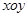 中
中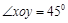 ,點
,點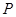 的斜坐標定義為:“若
的斜坐標定義為:“若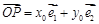 (其中
(其中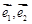 分別為與斜坐標系的
分別為與斜坐標系的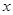 軸,
軸,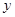 軸同方向的單位向量),則點
軸同方向的單位向量),則點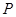 的坐標為
的坐標為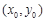 ”.若
”.若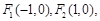 且動點
且動點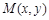 滿足
滿足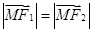 ,則點
,則點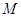 在斜坐標系中的軌跡方程為
在斜坐標系中的軌跡方程為
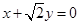
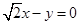

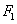 和
和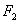 ,且|
,且|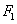
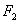 |=2,
|=2,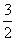 )在該橢圓上.
)在該橢圓上.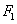 的直線
的直線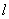 與橢圓C相交于A,B兩點,若
與橢圓C相交于A,B兩點,若 A
A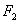 B的面積為
B的面積為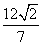 ,求以
,求以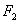 為圓心且與直線
為圓心且與直線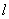 相切是圓的方程.
相切是圓的方程.