
【題目】如圖,在三棱錐P-ABC中,平面PAC⊥平面ABC,![]() 和
和![]() 都是正三角形,
都是正三角形,![]() , E、F分別是AC、BC的中點,且PD⊥AB于D.
, E、F分別是AC、BC的中點,且PD⊥AB于D.
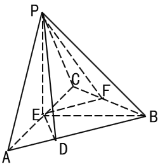
(Ⅰ)證明:直線![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)證明見解析(Ⅱ)![]()
【解析】
(Ⅰ)根據正三角形的性質和面面垂直的性質得![]() 面
面![]() ,繼而可得出
,繼而可得出![]() ,由線面垂直的判斷可得證;
,由線面垂直的判斷可得證;
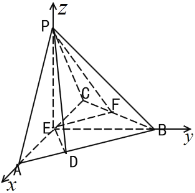
(Ⅱ)以點E為坐標原點,EA所在的直線為x軸,EB所在的直線為y軸,建立空間直角坐標系如圖示,,得出點![]() 的坐標,繼而求得面的法向量,根據二面角的坐標計算公式可得出二面角的正弦值.
的坐標,繼而求得面的法向量,根據二面角的坐標計算公式可得出二面角的正弦值.
(Ⅰ)∵E、F分別是AC、BC的中點,∴EF//AB,
在正三角形PAC中,PE⊥AC,又平面PAC⊥平面ABC,平面PAC![]() 平面ABC=AC,
平面ABC=AC,
∴PE⊥平面ABC,∴![]() 且PE⊥AB,又PD⊥AB,PE
且PE⊥AB,又PD⊥AB,PE![]() PD=P,
PD=P,
∴AB⊥平面PED, ![]() 又
又![]() //
//![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴直線![]() ⊥平面
⊥平面![]() .
.
(Ⅱ)∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BE⊥AC,
∴BE⊥平面PAC,
以點E為坐標原點,EA所在的直線為x軸,EB所在的直線為y軸,建立空間直角坐標系如圖示:
則![]() ,
,![]() ,
, ![]() ,
,
設![]() 為平面PAB的一個法向量,則由
為平面PAB的一個法向量,則由![]() 得
得
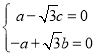 ,令
,令![]() ,得
,得![]() ,即
,即![]() ,
,
設二面角![]() 的大小為
的大小為![]() ,則
,則![]() ,則
,則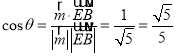 ,
,
![]() ,
,
即二面角![]() 的正弦值為
的正弦值為![]() .
.



 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
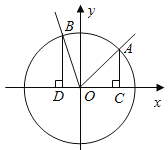
【題目】(本小題滿分13分)如圖,在直角坐標系![]() 中,角
中,角![]() 的頂點是原點,始邊與
的頂點是原點,始邊與![]() 軸正半軸重合.終邊交單位圓于點
軸正半軸重合.終邊交單位圓于點![]() ,且
,且![]() ,將角
,將角![]() 的終邊按逆時針方向旋轉
的終邊按逆時針方向旋轉![]() ,交單位圓于點
,交單位圓于點![]() ,記
,記![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分別過![]() 作
作![]() 軸的垂線,垂足依次為
軸的垂線,垂足依次為![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應國家號召,打贏脫貧致富攻堅戰,武漢大學團隊帶領湖北省大悟縣新城鎮熊灣村村民建立有機、健康、高端、綠色的蔬菜基地,并策劃“生產、運輸、銷售”一體化的直銷供應模式,據統計,當地村民兩年時間成功脫貧.蔬菜種植基地將采摘的有機蔬菜以每份三斤稱重并保鮮分裝,以每份10元的價格銷售到生鮮超市,每份15元的價格賣給顧客,如果當天前8小時賣不完,則超市通過促銷以每份5元的價格賣給顧客(根據經驗,當天能夠把剩余的有機蔬菜都低價處理完畢,且處理完畢后,當天不再進貨).該生鮮超市統計了100天有機蔬菜在每天的前8小時內的銷售量(單位:份),制成如下表格(注:![]() ,且
,且![]() ).若以100天記錄的頻率作為每日前8小時銷售量發生的概率,該生鮮超市當天銷售有機蔬菜利潤的期望值為決策依據,若購進17份比購進18份的利潤的期望值大,則x的最小值是________.
).若以100天記錄的頻率作為每日前8小時銷售量發生的概率,該生鮮超市當天銷售有機蔬菜利潤的期望值為決策依據,若購進17份比購進18份的利潤的期望值大,則x的最小值是________.
前8小時內銷售量 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
頻數 | 10 | x | 16 | 16 | 15 | 13 | y |
查看答案和解析>>
科目:高中數學 來源: 題型:
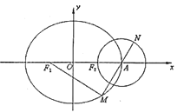
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,橢圓右頂點為
,橢圓右頂點為![]() ,點
,點![]() 在圓
在圓![]() :
:![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 在橢圓
在橢圓![]() 上,且位于第四象限,點
上,且位于第四象限,點![]() 在圓
在圓![]() 上,且位于第一象限,已知
上,且位于第一象限,已知![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
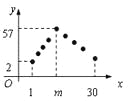
【題目】某專賣店銷售一新款服裝,日銷售量(單位為件)f(n) 與時間n(1≤n≤30、n![]() N*)的函數關系如下圖所示,其中函數f(n) 圖象中的點位于斜率為 5 和-3 的兩條直線上,兩直線交點的橫坐標為m,且第m天日銷售量最大.
N*)的函數關系如下圖所示,其中函數f(n) 圖象中的點位于斜率為 5 和-3 的兩條直線上,兩直線交點的橫坐標為m,且第m天日銷售量最大.
(Ⅰ)求f(n) 的表達式,及前m天的銷售總數;
(Ⅱ)按以往經驗,當該專賣店銷售某款服裝的總數超過 400 件時,市面上會流行該款服裝,而日銷售量連續下降并低于 30 件時,該款服裝將不再流行.試預測本款服裝在市面上流行的天數是否會超過 10 天?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
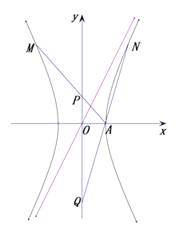
【題目】已知直線![]() 是雙曲線
是雙曲線![]() 的一條漸近線,點
的一條漸近線,點![]()
![]() 都在雙曲線
都在雙曲線![]() 上,直線
上,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,設坐標原點為
,設坐標原點為![]() .
.
(1)求雙曲線![]() 的方程,并求出點
的方程,并求出點![]() 的坐標(用
的坐標(用![]() 表示);
表示);
(2)設點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() .問:在
.問:在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)若過點![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,試求直線
,試求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() 函數
函數![]() ,函數
,函數![]() 的值域為
的值域為![]() ,
,
(1)若不等式![]() 的解集為
的解集為![]() ,求
,求![]() 的值;
的值;
(2)在(1)的條件下,若![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的不等式
的不等式![]() 的解集
的解集![]() ,求實數
,求實數![]() 的值
的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com