【題目】如圖，在四棱錐
中，
為等邊三角形，邊長為2，
為等腰直角三角形，
，
，
，平面
平面ABCD.
(1)證明：
平面PAD；
(2)求平面PAD與平面PBC所成銳二面角的余弦值；
(3)棱PD上是否存在一點E，使得
平面PBC？若存在，求出
的值；若不存在，請說明理由.
【答案】（1）證明見解析；（2）
；（3）棱PD上存在一點E，使得
平面PBC，且
.
【解析】
（1）用面面垂直的性質定理證明線面垂直；
（2）取
的中點
，連接
，得
平面
，以
為
軸，
為
軸，過
平行于的直線為
軸，建立如圖所示的空間直角坐標系，用平面的法向量的夾角求二面角；
（3）假設棱PD上存在一點E，使得平面PBC，設
，由
與平面
的法向量垂直求得
，如果求不出，說明不存在.
（1）∵平面
平面ABCD，
，平面
平面ABCD
，
平面ABCD，∴
平面
；
（2）取的中點，連接，由于
是等邊三角形，所以
，由平面平面ABCD，得平面，
，
以為軸，為軸，過平行于的直線為軸，建立如圖所示的空間直角坐標系，
則
，
，
，
，
，
，
，設平面
的一個法向量為
，
則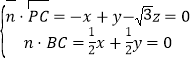
，取
，則
，
，
，
平面
的一個法向量為
，
，
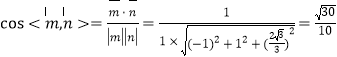∴平面PAD與平面PBC所成銳二面角的余弦值為；
（3）假設棱PD上存在一點E，使得平面PBC，設
，
由（2）
，
，
，又平面的一個法向量是，
∴
，解得
，∴.
∴棱PD上存在一點E，使得平面PBC，且.
優百分課時互動系列答案
開心蛙狀元作業系列答案科目：高中數學 來源： 題型：
【題目】某“雙一流A類”大學就業部從該校2018年已就業的大學本科畢業生中隨機抽取了100人進行問卷調查，其中一項是他們的月薪收入情況，調查發現，他們的月薪收入在人民幣1.65萬元到2.35萬元之間，根據統計數據分組，得到如下的頻率分布直方圖：
（1）為感謝同學們對這項調查工作的支持，該校利用分層抽樣的方法從樣本的前兩組中抽出6人，各贈送一份禮品，并從這6人中再抽取2人，各贈送某款智能手機1部，求獲贈智能手機的2人月薪都不低于1.75萬元的概率；
（2）同一組數據用該區間的中點值作代表.
（i）求這100人月薪收入的樣本平均數
和樣本方差
；
（ii）該校在某地區就業的2018屆本科畢業生共50人，決定于2019國慶長假期間舉辦一次同學聯誼會，并收取一定的活動費用，有兩種收費方案：
方案一：設
，月薪落在區間
左側的每人收取400元，月薪落在區間內的每人收到600元，月薪落在區間右側的每人收取800元.
方案二：按每人一個月薪水的3%收取；用該校就業部統計的這100人月薪收入的樣本頻率進行估算，哪一種收費方案能收到更多的費用？
參考數據：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某品牌布娃娃做促銷活動：已知有50個布娃娃，其中一些布娃娃里面有獎品，參與者可以先在50個布娃娃中購買5個，看完5個布娃娃里面的結果再決定是否將剩下的布娃娃全部購買，設每個布娃娃有獎品的概率為
，且各個布娃娃是否有獎品相互獨立.
（1）記5個布娃娃中有1個有獎品的概率為
，當
時，的最大值，求
；
（2）假如這5個布娃娃中恰有1個有獎品，以上問中的作為p的值.已知每次購買布娃娃需要2元，若有中獎，則中獎者每次可得獎金15元.以最終獎金的期望作為決策依據，是否該買下剩下所有的45個布娃娃；
（3）若已知50件布娃娃中有10個布娃娃有獎品，從這堆布娃娃中任意購買5個，若抽到k個有獎品可能性最大，求k的值.（k為正整數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某玩具廠擬定生產兩款新毛絨玩具樣品，一款為毛絨小豬，另一款為毛絨小狗．由設計圖知，生產這兩款毛絨玩具均需相同材質的填充物、長毛絨、天鵝絨，且每個毛絨小豬需填充物
、長毛絨
、天鵝絨
，每個毛絨小狗需填充物
、長毛絨
、天鵝絨
．現有所需填充物
、長毛絨
、天鵝絨
，若每個毛絨小豬與毛絨小狗的出廠價分別為64元、36元，則生這批毛絨玩具的最大銷售額為_______元．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱
中，四邊形ABCD為平行四邊形，
且點
在底面上的投影H恰為CD的中點.
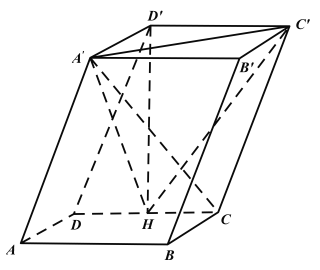
（1）棱BC上存在一點N，使得AD⊥平面
，試確定點N的位置，說明理由；
（2）求三棱錐
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
