
【題目】設函數![]() ,已知曲線
,已知曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行
平行
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在自然數![]() ,使得方程
,使得方程![]() 在
在![]() 內存在唯一的根?如果存在,求出
內存在唯一的根?如果存在,求出![]() ;如果不存在,請說明理由。
;如果不存在,請說明理由。
(Ⅲ)設函數![]() (
(![]() 表示
表示![]() 中的較小者),求
中的較小者),求![]() 的最大值。
的最大值。
【答案】(1) ![]() .
.
(2) ![]() 時,方程
時,方程![]() 在
在![]() 內存在唯一的根.證明見解析.
內存在唯一的根.證明見解析.
(3) ![]() .
.
【解析】試題分析:(Ⅰ)求出f(x)的導數,求得切線的斜率,由兩直線平行的條件:斜率相等,解方程可得![]() ;(Ⅱ)求出
;(Ⅱ)求出![]() 的導數和單調區間,最值,由零點存在定理,即可判斷存在
的導數和單調區間,最值,由零點存在定理,即可判斷存在![]() ;(Ⅲ)由(Ⅱ)求得
;(Ⅲ)由(Ⅱ)求得![]() 的解析式,通過
的解析式,通過![]() 的最大值,即可得到所求.
的最大值,即可得到所求.
試題解析:(Ⅰ)由題意知,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() ,所以
,所以![]() ,
,
又![]() 所以
所以![]() .
.
(Ⅱ)![]() 時,方程
時,方程![]() 在
在![]() 內存在唯一的根.
內存在唯一的根.
設![]()
當![]() 時,
時, ![]() .
.
又![]()
所以存在![]() ,使
,使![]() .
.
因為![]() 所以當
所以當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
所以當![]() 時,
時, ![]() 單調遞增.
單調遞增.
所以![]() 時,方程
時,方程![]() 在
在![]() 內存在唯一的根.
內存在唯一的根.
(Ⅲ)由(Ⅱ)知,方程![]() 在
在![]() 內存在唯一的根
內存在唯一的根![]() ,且
,且![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,所以
,所以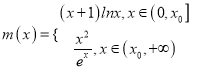 .
.
當![]() 時,若
時,若![]()
若![]() 由
由![]() 可知
可知![]() 故
故![]()
當![]() 時,由
時,由![]() 可得
可得![]() 時,
時, ![]() 單調遞增;
單調遞增; ![]() 時,
時, ![]() 單調遞減;
單調遞減;
可知![]() 且
且![]() .
.
綜上可得函數![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在正整數數列中,由1開始依次按如下規則取它的項:第一次取1;第二次取2個連續偶數2,4;第三次取3個連續奇數5,7,9;第四次取4個連續偶數10,12,14,16;第五次取5個連續奇數17,19,21,23,25,按此規律取下去,得到一個子數列1,2,4,5,7,9,10,12,14,16,17,19…,則在這個子數中第2014個數是( )
A. 3965 B. 3966 C. 3968 D. 3989
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣x2﹣ax.
(1)若曲線y=f(x)在點x=0處的切線斜率為1,求函數f(x)在[0,1]上的最值;
(2)令g(x)=f(x)+ ![]() (x2﹣a2),若x≥0時,g(x)≥0恒成立,求實數a的取值范圍;
(x2﹣a2),若x≥0時,g(x)≥0恒成立,求實數a的取值范圍;
(3)當a=0且x>0時,證明f(x)﹣ex≥xlnx﹣x2﹣x+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校的學生文娛團隊由理科組和文科組構成,具體數據如表所示:
組別 | 文科 | 理科 | ||
性別 | 男生 | 女生 | 男生 | 女生 |
人數 | 3 | 1 | 3 | 2 |
學校準備從該文娛團隊中選出4人到某社區參加大型公益活動演出,每選出一名男生,給其所在的組記1分;每選出一名女生,給其所在的組記2分,要求被選出的4人中文科組和理科組的學生都有.
(I)求理科組恰好得4分的概率;
(II)記文科組的得分為X,求隨機變量X的分布列和數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() . (I)求函數f(x)的單調區間;
. (I)求函數f(x)的單調區間;
(II)若不等式f(x)> ![]() 恒成立,求整數k的最大值;
恒成立,求整數k的最大值;
(III)求證:(1+1×2)(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:
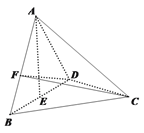
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() 都是邊長為
都是邊長為![]() 的等邊三角形,
的等邊三角形,![]() 為
為![]() 中點,且
中點,且![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上一動點,記
上一動點,記![]() .
.
(1)當![]() 時,求異面直線
時,求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)當![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中.側梭長均為4.底邊AC=4.AB=2,BC=2 ![]() ,D.E分別為PC.BC的中點. 〔I)求證:平面PAC⊥平面ABC.
,D.E分別為PC.BC的中點. 〔I)求證:平面PAC⊥平面ABC.
(Ⅱ)求三棱錐P﹣ABC的體積;
(Ⅲ)求二面角C﹣AD﹣E的余弦值.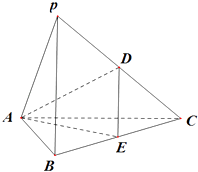
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com