
(本小題滿分16分)
已知數列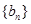 滿足
滿足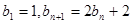 ,
,
(1)求證:數列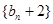 為等比數列 (2)求數列
為等比數列 (2)求數列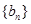 的通項公式
的通項公式
(3)試問:數列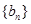 中是否存在不同的三項恰好成等差數列?若存在,求出這三項;若不存在,請說明理由.
中是否存在不同的三項恰好成等差數列?若存在,求出這三項;若不存在,請說明理由.
(1) ∵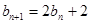 ,∴
,∴
所以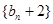 是以
是以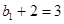 為首項,2為公比的等比數列....5分
為首項,2為公比的等比數列....5分
(2)  ...........10分
...........10分
(3)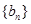 中不存在不同的三項
中不存在不同的三項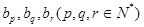 恰好成等差數列.
恰好成等差數列.
解析試題分析:(1)由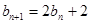 ,得
,得 ,
,
根據等比數列的定義可知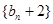 是等比數列.
是等比數列.
(2)在(1)的基礎上,可求出
(3)解本小題的關鍵:假設數列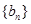 中存在不同的三項
中存在不同的三項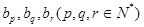 恰好成等差數列,顯然
恰好成等差數列,顯然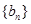 是遞增數列,然后可設
是遞增數列,然后可設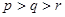 ,則
,則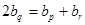 即
即 ,進而得到
,進而得到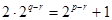 ,
,
然后再根據p,q,r取正整數值,并且還要從奇偶性判斷是否存在.
(1) ∵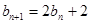 ,∴
,∴
所以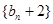 是以
是以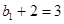 為首項,2為公比的等比數列....5分
為首項,2為公比的等比數列....5分
(2)  ...........10分
...........10分
(3)若數列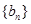 中存在不同的三項
中存在不同的三項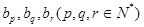 恰好成等差數列,顯然
恰好成等差數列,顯然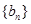 是遞增數列,不妨設
是遞增數列,不妨設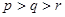 ,則
,則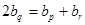
即 ,化簡得:
,化簡得: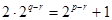 ……(*)................14分
……(*)................14分
由于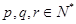 ,且
,且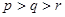 ,知
,知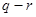 ≥1,
≥1, ≥2,
≥2,
所以(*)式左邊為偶數,右邊為奇數, 故數列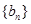 中不存在不同的三項
中不存在不同的三項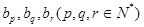 恰好成等差數列..16分
恰好成等差數列..16分
考點:等比數列的定義,與數列有關的探究性問題.
點評:等比數列的定義是判定一個數列是否是等比數列的依據,勿必理解掌握.對于探索性問題可先假設存在,然后根據條件探索存在應滿足的條件,從而最終得出結論.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)設遞增等比數列{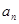 }的前n項和為
}的前n項和為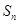 ,且
,且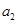 =3,
=3,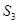 =13,數列{
=13,數列{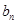 }滿足
}滿足 =
=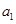 ,點P(
,點P(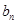 ,
,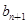 )在直線x-y+2=0上,n∈N﹡.
)在直線x-y+2=0上,n∈N﹡.
(Ⅰ)求數列{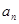 },{
},{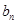 }的通項公式;
}的通項公式;
(Ⅱ)設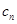 =
=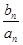 ,數列{
,數列{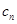 }的前n項和
}的前n項和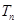 ,若
,若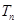 >2a-1恒成立(n∈N﹡),求實數a的取值范圍.
>2a-1恒成立(n∈N﹡),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12 分)
已知數列 為等比數列,且首項為
為等比數列,且首項為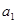 ,公比為
,公比為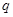 ,前
,前 項和為
項和為 .
.
(Ⅰ)試用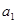 ,
,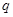 ,
, 表示前
表示前 項和
項和 ;
;
(Ⅱ)證明(Ⅰ)中所寫出的等比數列的前 項和公式。
項和公式。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)已知 是首項為19,公差d=-2的等差數列,
是首項為19,公差d=-2的等差數列, 為
為 的前n項和.(1)求通項公式
的前n項和.(1)求通項公式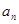 及
及 ;
;
(2)設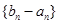 是首項為1,公比為3的等比數列,求數列
是首項為1,公比為3的等比數列,求數列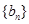 的通項公式及其前n項和
的通項公式及其前n項和
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列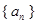 是首項為
是首項為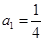 ,公比
,公比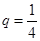 的等比數列. 設
的等比數列. 設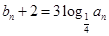
 ,數列
,數列 滿足
滿足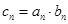 .
.
(Ⅰ)求證:數列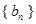 成等差數列;
成等差數列;
(Ⅱ)求數列 的前
的前 項和
項和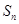 ;
;
(Ⅲ)若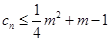 對一切正整數
對一切正整數 恒成立,求實數
恒成立,求實數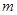 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com