
(本小題滿分12分)
已知關(guān)于 的不等式
的不等式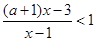 .
.
(Ⅰ)當(dāng) 時,解該不等式;
時,解該不等式;
(Ⅱ)當(dāng) 時,解該不等式.
時,解該不等式.
(Ⅰ)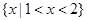 .
.
(Ⅱ)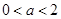 時,解集為
時,解集為 ,
,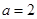 時,解集為
時,解集為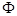 ,
,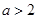 時,解集為
時,解集為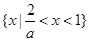
解析試題分析:這是一個含有字母系數(shù)的不等式,仔細觀察原不等式,通過去分母、移項并合并得到即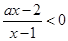 ,等價于
,等價于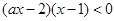 ,然后對于a進行分三類討論得到。
,然后對于a進行分三類討論得到。
解:原不等式可化為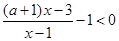 ,即
,即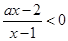 ,等價于
,等價于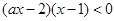
(Ⅰ)當(dāng) 時,不等式等價于
時,不等式等價于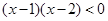 , ∴
, ∴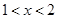
∴原不等式的解集為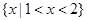 .
.
(Ⅱ)∵原不等式等價于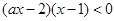 , ∴
, ∴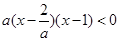
∵ , ∴
, ∴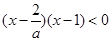
當(dāng)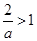 ,即
,即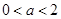 時,解集為
時,解集為
當(dāng)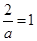 ,即
,即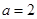 時,解集為
時,解集為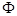
當(dāng)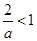 ,即
,即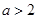 時,解集為
時,解集為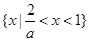
考點:本試題主要考查了不等式性質(zhì)的靈活運用,以及不等式的等價變形方法一般是移項通分合并,化分式不等式為整式不等式來解得。
點評:該試題主要考查了不等式的性質(zhì):(1)不等式的兩邊同時加上或減去同一個數(shù)或整式不等號的方向不變;(2)不等式的兩邊同時乘以或除以同一個正數(shù)不等號的方向不變;
(3)不等式的兩邊同時乘以或除以同一個負數(shù)不等號的方向改變.注意分三種情況討論.


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分10分)
設(shè)函數(shù)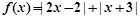 .
.
(1)解不等式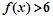 ;
;
(2)若關(guān)于的不等式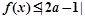 的解集不是空集,試求
的解集不是空集,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)
已知函數(shù)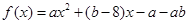 ,當(dāng)
,當(dāng)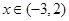 時,
時,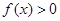 ;
;
當(dāng)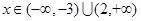 時,
時,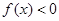 .
.
(1)求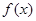 在
在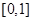 內(nèi)的值域;
內(nèi)的值域;
(2)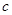 為何值時,
為何值時,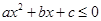 的解集為
的解集為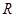 .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com