
如果對于任意一個三角形,只要它的三邊長 都在函數
都在函數 的定義域內,則
的定義域內,則  也是某個三角形的三邊長,則稱函數
也是某個三角形的三邊長,則稱函數 為“保三角形函數”.現有下列五個函數: ①
為“保三角形函數”.現有下列五個函數: ① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
則其中是 “保三角形函數”的有 .(寫出所有正確的序號)
①④
解析試題分析:滿足三角形的條件是兩邊之和大于第三邊,兩邊之差小于第三邊。
因為 是單調函數,且是自變量x的2倍,所以當三邊長
是單調函數,且是自變量x的2倍,所以當三邊長 都在函數
都在函數 的定義域內,2a,2b,2c,也極值函數定義域內,且滿足構成三角形的條件,所以①是;
的定義域內,2a,2b,2c,也極值函數定義域內,且滿足構成三角形的條件,所以①是;
②中,當三邊長 都在函數
都在函數 的定義域內,而
的定義域內,而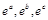 雖在函數定義域內,由于函數為增函數,且增大幅度的不同,不一定滿足構成三角形的條件,所以不是。
雖在函數定義域內,由于函數為增函數,且增大幅度的不同,不一定滿足構成三角形的條件,所以不是。
③中取 分別為3,4,5,則函數值分別為9,16,25,不能構成三角形,不是
分別為3,4,5,則函數值分別為9,16,25,不能構成三角形,不是
④f(x)= 是保三角形函數.
對任意一個三角形的三邊長a,b,c,則a+b>c,b+c>a,c+a>b,
f(a)= ,f(b)= ,f(c)= .
因為(+)2=a+2+b>c+2>()2,所以+>.
同理可以證明:+>,+>.
所以f(a)、f(b)、f(c)也是某個三角形的三邊長,故 f(x)= 是保三角形函數.
⑤ 在定義域內不單調,很明顯看出來,不是。綜上知是“保三角形函數”的有①④。
在定義域內不單調,很明顯看出來,不是。綜上知是“保三角形函數”的有①④。
考點:本題主要考查常見函數的圖象和性質,構成三角形的條件,學習能力。
點評:難題,本題是新定義問題,作為填空題,可以通過舉反例排除,集合函數圖象“猜測”判斷。作為解析該題,則為難題。


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:填空題
關于函數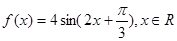 有下列命題:
有下列命題:
(1)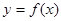 的表達式可改寫為
的表達式可改寫為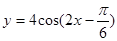 ;
;
(2)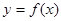 是以
是以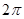 為最小正周期的周期函數;
為最小正周期的周期函數;
(3)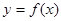 的圖象關于點
的圖象關于點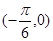 對稱;
對稱;
(4)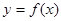 的圖象關于直線
的圖象關于直線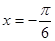 對稱。
對稱。
其中正確的命題序號是 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com