
已知函數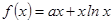 的圖象在點
的圖象在點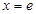 (e為自然對數的底數)處取得極值-1.
(e為自然對數的底數)處取得極值-1.
(1)求實數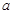 的值;
的值;
(2)若不等式 對任意
對任意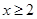 恒成立,求
恒成立,求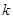 的取值范圍.
的取值范圍.
(1)-2;(2)
解析試題分析:(1)因為函數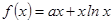 的圖象在點
的圖象在點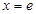 (e為自然對數的底數)處取得極值-1,所以
(e為自然對數的底數)處取得極值-1,所以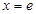 時導函數的值為零.即可求出
時導函數的值為零.即可求出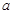 的值.
的值.
(2)因為不等式 對任意
對任意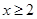 恒成立,所以寫出等價的不等式,從而轉化為求函數的在
恒成立,所以寫出等價的不等式,從而轉化為求函數的在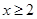 時的最小值的問題.所以通過對函數的求導,觀察發現函數的單調性即可得到函數的在
時的最小值的問題.所以通過對函數的求導,觀察發現函數的單調性即可得到函數的在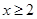 范圍的最小值.從而得到結論.
范圍的最小值.從而得到結論.
試題解析:(1)解:因為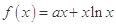 ,所以
,所以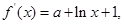
因為函數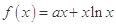 的圖像在點
的圖像在點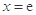 處取得極值,
處取得極值,
所以 . 4分
. 4分
(2)解:由(1)知,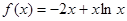 ,
,
所以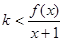 對任意
對任意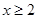 恒成立,即
恒成立,即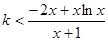 對任意
對任意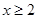 恒成立.
恒成立.
令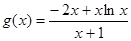 ,則,
,則,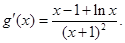
因為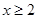 ,所以
,所以 ,
,
所以函數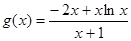 在
在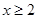 上為增函數,
上為增函數,
則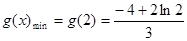 ,
,
所以 . 12分
. 12分
考點:1.函數的極值.2.函數的最值問題.3.不等式的恒成立問題.4.數形結合的思想.


科目:高中數學 來源: 題型:解答題
已知兩函數f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k為實數.
(1)對任意x∈[-3,3]都有f(x)≤g(x)成立,求k的取值范圍.
(2)存在x∈[-3,3]使f(x)≤g(x)成立,求k的取值范圍.
(3)對任意x1,x2∈[-3,3]都有f(x1)≤g(x2),求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經市場調查,某旅游城市在過去的一個月內(以30天計),旅游人數f(t)(萬人)與時間t(天)的函數關系近似滿足f(t)=4+ ,人均消費g(t)(元)與時間t(天)的函數關系近似滿足g(t)=115-|t-15|.
,人均消費g(t)(元)與時間t(天)的函數關系近似滿足g(t)=115-|t-15|.
(1)求該城市的旅游日收益w(t)(萬元)與時間t(1≤t≤30,t∈N*)的函數關系式;
(2)求該城市旅游日收益的最小值(萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數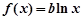 ,
,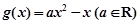
(1)若曲線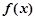 與
與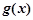 在公共點
在公共點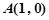 處有相同的切線,求實數
處有相同的切線,求實數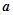 、
、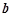 的值;
的值;
(2)當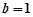 時,若曲線
時,若曲線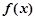 與
與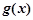 在公共點
在公共點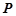 處有相同的切線,求證:點
處有相同的切線,求證:點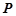 唯一;
唯一;
(3)若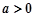 ,
,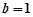 ,且曲線
,且曲線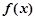 與
與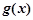 總存在公切線,求正實數
總存在公切線,求正實數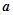 的最小值
的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
若函數f(x)對任意的實數x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,則稱函數f(x)是區間D上的“平緩函數”.
(1)判斷g(x)=sin x和h(x)=x2-x是不是實數集R上的“平緩函數”,并說明理由;
(2)若數列{xn}對所有的正整數n都有|xn+1-xn|≤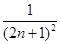 ,設yn=sin xn,求證:|yn+1-y1|<
,設yn=sin xn,求證:|yn+1-y1|< .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的定義域為
的定義域為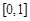 ,且
,且 的圖象連續不間斷. 若函數
的圖象連續不間斷. 若函數 滿足:對于給定的
滿足:對于給定的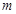 (
(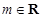 且
且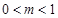 ),存在
),存在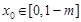 ,使得
,使得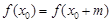 ,則稱
,則稱 具有性質
具有性質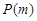 .
.
(1)已知函數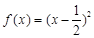 ,
,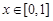 ,判斷
,判斷 是否具有性質
是否具有性質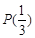 ,并說明理由;
,并說明理由;
(2)已知函數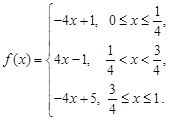 若
若 具有性質
具有性質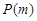 ,求
,求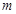 的最大值;
的最大值;
(3)若函數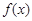 的定義域為
的定義域為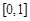 ,且
,且 的圖象連續不間斷,又滿足
的圖象連續不間斷,又滿足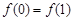 ,
,
求證:對任意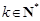 且
且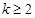 ,函數
,函數 具有性質
具有性質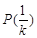 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
心理學家通過研究學生的學習行為發現;學生的接受能力與老師引入概念和描述問題所用的時間相關,教學開始時,學生的興趣激增,學生的興趣保持一段較理想的狀態,隨后學生的注意力開始分散,分析結果和實驗表明,用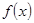 表示學生掌握和接受概念的能力, x表示講授概念的時間(單位:min),可有以下的關系:
表示學生掌握和接受概念的能力, x表示講授概念的時間(單位:min),可有以下的關系: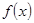
(1)開講后第5min與開講后第20min比較,學生的接受能力何時更強一些?
(2)開講后多少min學生的接受能力最強?能維持多少時間?
(3)若一個新數學概念需要55以上(包括55)的接受能力以及13min時間,那么老師能否在學生一直達到所需接受能力的狀態下講授完這個概念?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
噪聲污染已經成為影響人們身體健康和生活質量的嚴重問題.實踐證明,聲音強度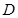 (分貝)由公式
(分貝)由公式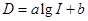 (
(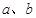 為非零常數)給出,其中
為非零常數)給出,其中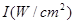 為聲音能量.
為聲音能量.
(1)當聲音強度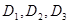 滿足
滿足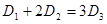 時,求對應的聲音能量
時,求對應的聲音能量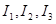 滿足的等量關系式;
滿足的等量關系式;
(2)當人們低聲說話,聲音能量為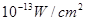 時,聲音強度為30分貝;當人們正常說話,聲音能量為
時,聲音強度為30分貝;當人們正常說話,聲音能量為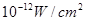 時,聲音強度為40分貝.當聲音能量大于60分貝時屬于噪音,一般人在100分貝~120分貝的空間內,一分鐘就會暫時性失聰.問聲音能量在什么范圍時,人會暫時性失聰.
時,聲音強度為40分貝.當聲音能量大于60分貝時屬于噪音,一般人在100分貝~120分貝的空間內,一分鐘就會暫時性失聰.問聲音能量在什么范圍時,人會暫時性失聰.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com