
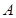 、
、 、
、 、
、 、
、 ,它的一個面
,它的一個面 內接于⊙
內接于⊙ ,
, 是⊙
是⊙ 的直徑,四邊形
的直徑,四邊形 為平行四邊形,
為平行四邊形, 平面
平面 .
.
 平面
平面 ;
; ,
, ,
, ,求該簡單幾何體的體積.
,求該簡單幾何體的體積.
 平面
平面
 平面
平面 ,
, 平面
平面 ,
, . ………1分
. ………1分 是⊙
是⊙ 的直徑,
的直徑,
 , ………2分
, ………2分 ………3分
………3分 平面
平面 , ………4分
, ………4分
 平面
平面 ………5分
………5分 平面
平面 ………6分
………6分 平面
平面
 平面
平面 . ………7分
. ………7分 ,
,
 平面
平面
 平面
平面
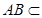 平面
平面


 中
中

 ………8分
………8分 ,由(1),(2)知
,由(1),(2)知 是三棱錐
是三棱錐 的高,
的高, 是三棱錐
是三棱錐 的高
的高 ………9分
………9分 ………11分
………11分 ………13分
………13分 該簡單組合體的體積
該簡單組合體的體積 . ………14分
. ………14分 平面
平面 ,
,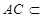 平面
平面 ,
, .
.  ,
, 
 平面
平面 ,
,  是四棱錐
是四棱錐 的高,且由(1),(2)證明易知四邊形
的高,且由(1),(2)證明易知四邊形 為邊長為
為邊長為 的正方形. ………10分
的正方形. ………10分 ………11分
………11分 ………12分
………12分 ………13分
………13分
 ………14分
………14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com