
【題目】已知函數![]() .
.
(Ⅰ)若![]() ,討論
,討論![]() 的單調性;
的單調性;
(Ⅱ)若函數![]() 的圖象上存在不同的兩點
的圖象上存在不同的兩點![]() ,使得直線
,使得直線![]() 的斜率
的斜率![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)當![]() 時,
時, ![]() 的減區間是
的減區間是![]() ,無增區間,當
,無增區間,當![]() 時,
時, ![]() 的增區間是
的增區間是![]() ,減區間是
,減區間是![]() ,當
,當![]() 時,
時, ![]() 的增區間是
的增區間是![]() ,減區間是
,減區間是![]() .
.
(Ⅱ)![]() 。
。
【解析】試題分析:(Ⅰ)先求函數![]() 的導數,再對參數
的導數,再對參數![]() 進行分類討論,分別確定其單調性并求出其單調區間,(Ⅱ)先運用斜率公式將不等式等價轉化為
進行分類討論,分別確定其單調性并求出其單調區間,(Ⅱ)先運用斜率公式將不等式等價轉化為![]() ,進而轉化為不等式
,進而轉化為不等式![]() 恒成立,然后構造函數
恒成立,然后構造函數![]() ,借助導數及其單調性建立不等式
,借助導數及其單調性建立不等式![]() 進行求解:
進行求解:
解:(Ⅰ) ![]() 的定義域為
的定義域為![]() ,當
,當![]() 時,
時, ![]()
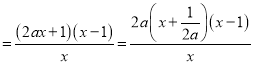 ,
,
(ⅰ)若![]() ,即
,即![]() 時,
時, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上是減函數;
上是減函數;
(ⅱ)若![]() ,即
,即![]() 時,
時, ![]() 時
時![]() ,
, ![]() 是增函數,
是增函數,
![]() 時,
時, ![]() ,
, ![]() 是減函數,
是減函數,
![]() 時,
時, ![]() ,
, ![]() 是減函數;
是減函數;
(ⅲ)若![]() ,即
,即![]() ,
, ![]() 時,
時, ![]() ,
, ![]() 是增函數,
是增函數,
![]() 時,
時, ![]() ,
, ![]() 是減函數,
是減函數,
![]() 時,
時, ![]() ,
, ![]() 是減函數;
是減函數;
綜上可得,當![]() 時,
時, ![]() 的減區間是
的減區間是![]() ,無增區間,
,無增區間,
當![]() 時,
時, ![]() 的增區間是
的增區間是![]() ,減區間是
,減區間是![]() ,
,
當![]() 時,
時, ![]() 的增區間是
的增區間是![]() ,減區間是
,減區間是![]() .
.
(Ⅱ)假設![]() 的圖象上不存在兩點
的圖象上不存在兩點![]() ,使得直線
,使得直線![]() 的斜率
的斜率![]() 成立,
成立,
則對![]() 的圖象上任意兩點
的圖象上任意兩點![]() ,都有
,都有![]() 成立,
成立,
即![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
因為![]() ,所以
,所以![]() ,
,
所以![]() 是減函數,
是減函數, ![]() 恒成立,
恒成立,
因為![]() ,所以
,所以![]() 恒成立,
恒成立,
因為![]() ,所以
,所以![]() .
.
即若對![]() 的圖象上任意兩點
的圖象上任意兩點![]() ,都有
,都有![]() 成立,則
成立,則![]() ,
,
所以若![]() 的圖象上不存在兩點
的圖象上不存在兩點![]() ,使得直線
,使得直線![]() 的斜率
的斜率![]() 成立,
成立,
則![]() ,即實數
,即實數![]() 的取值范圍是
的取值范圍是![]() .
.


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源: 題型:
【題目】有兩個命題,p:關于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函數y=lg(ax2﹣x+a)的定義域為R.如果p∨q為真命題,p∧q為假命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:極坐標與參數方程
在平面直角坐標系xoy中,曲線![]() ,直線
,直線![]() 過點
過點![]() 與曲線
與曲線![]() 交于
交于![]() 二點,
二點, ![]() 為
為![]() 中點.以坐標原點O為極點,x軸正半軸為極軸,以平面直角坐標系xoy的單位1為基本單位建立極坐標系.
中點.以坐標原點O為極點,x軸正半軸為極軸,以平面直角坐標系xoy的單位1為基本單位建立極坐標系.
(1)求直線![]() 的極坐標方程;
的極坐標方程;
(2) ![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,| ![]() |=|
|=| ![]() |=|
|=| ![]() |=1,
|=1, ![]() ,A(1,1),則
,A(1,1),則 ![]() 的取值范圍( )
的取值范圍( )
A.[﹣1﹣ ![]() ,
, ![]() ﹣1]
﹣1]
B.[﹣ ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() +
+ ![]() ]?
]?
C.[ ![]() ﹣
﹣ ![]() ,
, ![]() +
+ ![]() ]
]
D.[1﹣ ![]() ,1+
,1+ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:關于x的不等式x2+2ax+4>0對一切x∈R恒成立;命題q:函數f(x)=lagax在(0,+∞)上遞增,若p∨q為真,而p∧q為假,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠的打印機每5年需淘汰一批舊打印機并購買新機,買新機時,同時購買墨盒,每臺新機隨機購買第一盒墨150元,優惠0元;再每多買一盒墨都要在原優惠基礎上多優惠一元,即第一盒墨沒有優惠,第二盒墨優惠一元,第三盒墨優惠2元,……,依此類推,每臺新機最多可隨新機購買25盒墨.平時購買墨盒按零售每盒200元.
公司根據以往的記錄,十臺打印機正常工作五年消耗墨盒數如下表:
消耗墨盒數 | 22 | 23 | 24 | 25 |
打印機臺數 | 1 | 4 | 4 | 1 |
以這十臺打印機消耗墨盒數的頻率代替一臺打印機消耗墨盒數發生的概率,記ξ表示兩臺打印機5年消耗的墨盒數.
(1)求ξ的分布列;
(2)若在購買兩臺新機時,每臺機隨機購買23盒墨,求這兩臺打印機正常使用五年在消耗墨盒上所需費用的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:y=4x和點P(6,4),點A為第一象限內的點且在直線l上,直線PA交x軸正半軸于點B,
(1)當OP⊥AB時,求AB所在直線的直線方程;
(2)求△OAB面積的最小值,并求當△OAB面積取最小值時的B的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com