
【題目】將一張紙沿直線l對(duì)折一次后,點(diǎn)A(0,4)與點(diǎn)B(8,0)重疊,點(diǎn)C(6,8)與點(diǎn)D(m,n)重疊.
(1)求直線l的方程;
(2)求m+n的值;
(3)直線l上是否存在一點(diǎn)P,使得||PB|﹣|PC||存在最大值,如果存在,請(qǐng)求出最大值,以及此時(shí)點(diǎn)P的坐標(biāo);如果不存在,請(qǐng)說(shuō)明理由.
【答案】
(1)解:設(shè)線段AB的中點(diǎn)為N,則點(diǎn)N(4,2),且 ![]()
則直線l的方程為2x﹣y﹣6=0
(2)解:設(shè)直線CD的方程為x+2y+C'=0
∵C(6,8)在直線CD上,∴C'=﹣22,則直線CD的方程為x+2y﹣22=0
設(shè)直線CD與直線l的交點(diǎn)為M, ![]()
![]()
則 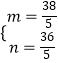 ,∴
,∴ ![]()
(3)解:假設(shè)直線l上存在點(diǎn)P,
∵||PB|﹣|PC||=||PA|﹣|PC||≥|AC|
當(dāng)且僅當(dāng)P,A,C三點(diǎn)共線時(shí),等號(hào)成立
直線AC的方程為x﹣3y+12=0
∴ ![]() ,∴P(6,6)
,∴P(6,6)
【解析】(1)設(shè)線段AB的中點(diǎn)為N,則點(diǎn)N(4,2),且 ![]() ,即可求出直線l的方程;(2)求出直線CD的方程,可得直線CD與直線l的交點(diǎn)坐標(biāo),即可求m+n的值;(3)假設(shè)直線l上存在點(diǎn)P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出結(jié)論.
,即可求出直線l的方程;(2)求出直線CD的方程,可得直線CD與直線l的交點(diǎn)坐標(biāo),即可求m+n的值;(3)假設(shè)直線l上存在點(diǎn)P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出結(jié)論.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我們把b除a的余數(shù)r記為r=abmodb,例如4=9bmod5,如圖所示,若輸入a=209,b=77,則循環(huán)體“r←abmodb”被執(zhí)行了次. 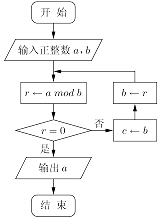
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列各函數(shù)在其定義域中,既是奇函數(shù),又是增函數(shù)的是( )
A.y=x+1
B.y=﹣x3
C.y=﹣ ![]()
D.y=x|x|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若Ai(i=1,2,3,…,n)是△AOB所在平面內(nèi)的點(diǎn),且 ![]()
![]() =
= ![]()
![]() ,給出下列說(shuō)法:
,給出下列說(shuō)法:
·(1)| ![]() |=|
|=| ![]() |=|
|=| ![]() |=…=|
|=…=| ![]() |
|
·(2)| ![]() |的最小值一定是|
|的最小值一定是| ![]() |
|
·(3)點(diǎn)A和點(diǎn)Ai一定共線
·(4)向量 ![]() 及
及 ![]() 在向量
在向量 ![]() 方向上的投影必定相等
方向上的投影必定相等
其中正確的個(gè)數(shù)是( )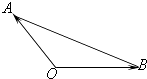
A.1個(gè)
B.2個(gè)
C.3個(gè)
D.4個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)y=lg(3﹣4x+x2)的定義域?yàn)镸,當(dāng)x∈M時(shí),則f(x)=2x+2﹣3×4x的最大值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若函數(shù)f(x)定義在R上的奇函數(shù),且在(﹣∞,0)上是增函數(shù),又f(2)=0,則不等式xf(x+1)<0的解集為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若不等式x2﹣ax+b<0的解集為(1,2),則不等式 ![]() <
< ![]() 的解集為( )
的解集為( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
C.( ![]() ,+∞)
,+∞)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com