
已知函數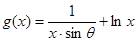 在[1,+∞)上為增函數,且
在[1,+∞)上為增函數,且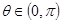 ,
,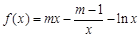 ,
, ∈R.
∈R.
(1)求θ的值;
(2)若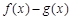 在[1,+∞)上為單調函數,求m的取值范圍;
在[1,+∞)上為單調函數,求m的取值范圍;
(3)設 ,若在[1,e]上至少存在一個
,若在[1,e]上至少存在一個 ,使得
,使得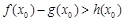 成立,求
成立,求 的取值范圍.
的取值范圍.
(1)由題意,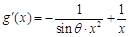 ≥0在
≥0在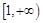 上恒成立,即
上恒成立,即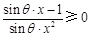 .
.
∵θ∈(0,π),∴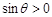 .故
.故 在
在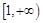 上恒成立,
上恒成立,
只須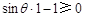 ,即
,即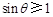 ,只有
,只有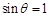 .結合θ∈(0,π),得
.結合θ∈(0,π),得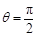 .…4分
.…4分
(2)由(1),得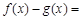
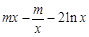 .
.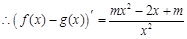 .
.
∵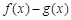 在其定義域內為單調函數,
在其定義域內為單調函數,
∴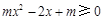 或者
或者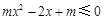 在[1,+∞)恒成立.…………6分
在[1,+∞)恒成立.…………6分
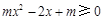 等價于
等價于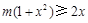 ,即
,即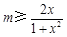 ,
,
而 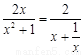 ,(
,(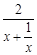 )max=1,∴
)max=1,∴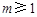 . ………………………7分
. ………………………7分
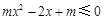 等價于
等價于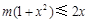 ,即
,即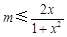 在[1,+∞)恒成立,
在[1,+∞)恒成立,
而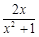 ∈(0,1],
∈(0,1],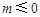 .
.
綜上,m的取值范圍是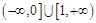 .……………………………9分
.……………………………9分
(3)構造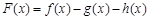 ,
,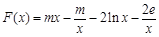 .
.
當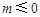 時,
時,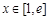 ,
,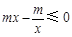 ,
,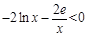 ,所以在[1,e]上不存在一個
,所以在[1,e]上不存在一個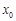 使得
使得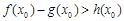 成立. ………………………………11分
成立. ………………………………11分
當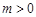 時,
時,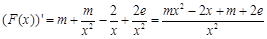 .
.
因為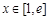 ,所以
,所以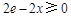 ,
,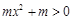 ,所以
,所以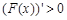 在
在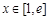 恒成立.
恒成立.
故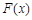 在
在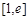 上單調遞增,
上單調遞增,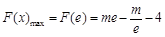 ,只要
,只要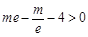 ,
,
解得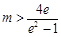
故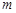 的取值范圍是
的取值范圍是 .
.
【解析】略


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2011-2012學年浙江省高三上學期期中理科數學試卷 題型:解答題
已知函數 在[1,+∞)上為增函數,且
在[1,+∞)上為增函數,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若 在[1,+∞)上為單調函數,求m的取值范圍;
在[1,+∞)上為單調函數,求m的取值范圍;
(3)設 ,若在[1,e]上至少存在一個
,若在[1,e]上至少存在一個 ,使得
,使得 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省杭州市求是高復高三11月月考文科數學 題型:解答題
(本題滿分15分)
已知函數 在[1,+∞)上為增函數,且
在[1,+∞)上為增函數,且 ,
,
(1)求 的值;
的值;
(2)若 在[1,+∞)上為單調函數,求實數
在[1,+∞)上為單調函數,求實數 的取值范圍;
的取值范圍;
(3)若在 上至少存在一個
上至少存在一個 ,使得
,使得 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com