(8分)設a>b>c,求證：bc2+ca2+ab2<b2c+c2a+a2b.
中考解讀考點精練系列答案
各地期末復習特訓卷系列答案科目：高中數學 來源：2011-2012學年山東省高三下學期模擬預測文科數學試卷（解析版） 題型：解答題
設函數f（x）=lnx，g（x）=ax+
，函數f（x）的圖像與x軸的交點也在函數g（x）的圖像上，且在此點處f（x）與g（x）有公切線.[來源:學。科。網]
（Ⅰ）求a、b的值；
（Ⅱ）設x>0，試比較f（x）與g（x）的大小.[來源:學,科,網Z,X,X,K]
【解析】第一問解：因為f（x）=lnx，g（x）=ax+
則其導數為
由題意得，
第二問，由（I）可知
，令
。
∵
， …………8分
∴
是（0，+∞）上的減函數，而F（1）=0， …………9分
∴當
時，
，有
；當
時，
，有
；當x=1時，
，有
解：因為f（x）=lnx，g（x）=ax+
則其導數為
由題意得，
（11）由（I）可知，令
。
∵
， …………8分
∴是（0，+∞）上的減函數，而F（1）=0， …………9分
∴當時，，有；當時，，有；當x=1時，，有
查看答案和解析>>
科目：高中數學 來源：2011-2012學年上海市長寧區高三教學質量測試理科數學 題型：解答題
本小題滿分18分) 本題共有3個小題，第1小題滿分4分，第2小題滿分6分，第3小題滿分8分.
設函數
是定義域為R的奇函數．
（1）求k值；
（2）（文）當
時，試判斷函數單調性并求不等式f(x2＋2x)＋f(x－4)>0的解集；
（理）若f(1)<0，試判斷函數單調性并求使不等式
恒成立的
的取值范圍；
（3）若f(1)＝，且g(x)＝a 2x＋a - 2x－2m f(x) 在[1，＋∞)上的最小值為－2，求m的值．
查看答案和解析>>
科目：高中數學 來源：2010年海南省高一期中考試數學試卷 題型：解答題
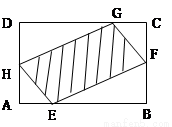
（本題滿分8分）如圖，有一塊矩形空地，要在這塊空地上辟一個內接四邊形為綠地，使其四個頂點分別落在矩形的四條邊上，已知AB＝a（a>2），BC＝2，且AE＝AH＝CF＝CG，設AE＝x，綠地面積為y．
(Ⅰ)寫出y關于x的函數關系式，并指出這個函數的定義域；
(Ⅱ)當AE為何值時，綠地面積最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
（本題滿分18分）本題共有3個小題，第1小題滿分3分，第2小題滿分7分，第3小題滿分8分）
由函數y=f（x）確定數列{an}，an=f（n），函數y=f（x）的反函數y=f －1（x）能確定數列{bn}，bn= f –1（n），若對于任意nÎN*，都有bn=an，則稱數列{bn}是數列{an}的“自反數列”．
（1）若函數f（x）=確定數列{an}的自反數列為{bn}，求an；
（2）已知正數數列{cn}的前n項之和Sn=（cn+）．寫出Sn表達式，并證明你的結論；
（3）在（1）和（2）的條件下，d1=2，當n≥2時，設dn=，Dn是數列{dn}的前n項之和，且Dn>log a （1－2a）恒成立，求a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
