Question

關于的方程，給出下列四個題：
①存在實數，使得方程恰有2個不同的實根；
②存在實數，使得方程恰有4個不同的實根；
③存在實數，使得方程恰有5個不同的實根；
④存在實數，使得方程恰有8個不同的實根。
正確命題的序號為           

Answer 1

①②③④

解析試題分析：關于x的方程（x²-1）²-|x²-1|+k=0可化為（x²-1）²-（x²-1）+k=0（x≥1或x≤-1）（1）

或（x²-1）²+（x²-1）+k=0（-1＜x＜1）（2）
當k=-2時，方程（1）的解為±，方程（2）無解，原方程恰有2個不同的實根
當k=時，方程（1）有兩個不同的實根±，方程（2）有兩個不同的實根±，
即原方程恰有4個不同的實根
當k=0時，方程（1）的解為-1，+1，±，方程（2）的解為x=0，原方程恰有5個不同的實根當k=時，方程（1）的解為±，±，方程（2）的解為±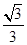，±，即原方程恰有8個不同的實根，∴四個命題都是真命題，故填寫①②③④，
考點：本題主要是考查了分段函數，以及函數與方程的思想，數形結合的思想，同時考查了分析問題的能力，屬于中檔題
點評：解決該試題的關鍵是將方程根的問題轉化成函數圖象的問題，畫出函數圖象，結合圖象可得結論