Question

（本題滿分12分）已知橢圓C：的焦點在y軸上，且離心率為．過點M(0，3)的直線l與橢圓C相交于兩點A、B．    （1）求橢圓C的方程；（2）設P為橢圓上一點，且滿足（O為坐標原點），當||<時，求實數λ的取值范圍．

Answer 1

(Ⅰ)    (Ⅱ)  (-2，)∪(，2)

解析:

（1）由題知a²=m，b²=1，∴ c²=m-1∴ ，解得m=4．

∴ 橢圓的方程為．……4分

（2）當l的斜率不存在時，，不符合條件． ………5分

設l的斜率為k，則l的方程為y=kx+3．

設A(x₁，y₁)，B(x₂，y₂)，P(x₀，y₀)，

聯立l和橢圓的方程：  消去y，整理得(4+k²)x²+6kx+5=0，

∴ Δ=(6k)²-4×(4+k²)×5=16k²-80>0，解得k²>5．

且，

∴ =，

由已知有，整理得13k⁴-88k²-128<0，解得 ，

∴ 5<k²<8．……9分∵ ，即(x₁，y₂)+(x₂，y₂)= λ(x₀，y₀)，

∴ x₁+x₂=λx₀，y₁+y₂₌λy₀，

當λ=0時，x₁+x₂=，，

顯然，上述方程無解．

當λ≠0時，=，．

∵ P(x₀，y₀)在橢圓上，∴ ，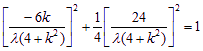

化簡得．由 5<k²<8，可得3<²<4，∴ λ∈(-2，-)∪(，2)．

即λ的取值范圍為(-2，)∪(，2)……12分