
【題目】設甲、乙、丙三個乒乓球協會的分別選派3,1,2名運動員參加某次比賽,甲協會運動員編號分別為A1 , A2 , A3 , 乙協會編號為A4 , 丙協會編號分別為A5 , A6 , 若從這6名運動員中隨機抽取2名參加雙打比賽.
(1)用所給編號列出所有可能抽取的結果;
(2)求丙協會至少有一名運動員參加雙打比賽的概率;
(3)求參加雙打比賽的兩名運動員來自同一協會的概率.
【答案】
(1)解:從這6名運動員中隨機抽取2名參加雙打比賽,
所有可能的結果為{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},
{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},
{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15種
(2)解:∵丙協會至少有一名運動員參加雙打比賽,
∴編號為A5,A6的兩名運動員至少有一人被抽到,
其結果為:{A1,A5},{A1,A6},{A2,A5},{A2,A6},{A3,A5},
{A3,A6},{A4,A5},{A4,A6},{A5,A6},共9種,
∴丙協會至少有一名運動員參加雙打比賽的概率P(A)= ![]()
(3)解:兩名運動員來自同一協會有{A1,A2},{A1,A3},{A2,A3},{A5,A6}共4種
參加雙打比賽的兩名運動員來自同一協會的概率為 ![]()
【解析】(1)從這6名運動員中隨機抽取2名參加雙打比賽,利用列舉法能求出所有可能的結果.(2)由丙協會至少有一名運動員參加雙打比賽,知編號為A5 , A6的兩名運動員至少有一人被抽到,由此利用列舉法能求出丙協會至少有一名運動員參加雙打比賽的概率.(3)由列舉法得兩名運動員來自同一協會有4種,由此能求出參加雙打比賽的兩名運動員來自同一協會的概率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )在一個周期內的圖像如圖所示,其中M(
)在一個周期內的圖像如圖所示,其中M( ![]() ,2),N(
,2),N( ![]() ,0).
,0). 
(1)求函數f(x)的解析式;
(2)在△ABC中,角A,B,C的對邊分別是a,b,c,且a= ![]() ,c=3,f(
,c=3,f( ![]() )=
)= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)當x∈[2,3]時,求函數f(x)的值域(用t表示)
(2)設集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整數t,使得A∩B=A.若存在,請求出所有可能的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知動點
中,已知動點![]() 到定點
到定點![]() 的距離與到定直線
的距離與到定直線![]() 的距離之比為
的距離之比為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 為定直線
為定直線![]() 上一點.
上一點.
①過點![]() 作
作![]() 的垂線交軌跡
的垂線交軌跡![]() 于點
于點![]() (
(![]() 不在
不在![]() 軸上),求證:直線
軸上),求證:直線![]() 與
與![]() 的斜率之積是定值;
的斜率之積是定值;
②若點![]() 的坐標為
的坐標為![]() ,過點
,過點![]() 作動直線
作動直線![]() 交軌跡
交軌跡![]() 于不同兩點
于不同兩點![]() ,線段
,線段![]() 上的點
上的點![]() 滿足
滿足![]() ,求證:點
,求證:點![]() 恒在一條定直線上.
恒在一條定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某景區修建一棟復古建筑,其窗戶設計如圖所示.圓![]() 的圓心與矩形
的圓心與矩形![]() 對角線的交點重合,且圓與矩形上下兩邊相切(
對角線的交點重合,且圓與矩形上下兩邊相切(![]() 為上切點),與左右兩邊相交(
為上切點),與左右兩邊相交(![]() ,
, ![]() 為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1m,且
為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1m,且![]() .設
.設![]() ,透光區域的面積為
,透光區域的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式,并求出定義域;
的函數關系式,并求出定義域;
(2)根據設計要求,透光區域與矩形窗面的面積比值越大越好.當該比值最大時,求邊![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C為三角形ABC的三內角,其對應邊分別為a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;
(2)若 ![]() ,b+c=4,求三角形ABC的面積.
,b+c=4,求三角形ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信運動和運動手環的普及,增強了人民運動的積極性,每天一萬步稱為一種健康時尚,某中學在全校范圍內內積極倡導和督促師生開展“每天一萬步”活動,經過幾個月的扎實落地工作后,學校想了解全校師生每天一萬步的情況,學校界定一人一天走路不足![]() 千步為不健康生活方式,不少于
千步為不健康生活方式,不少于![]() 千步為超健康生活方式者,其他為一般生活方式者,學校委托數學組調查,數學組采用分層抽樣的辦法去估計全校師生的情況,結合實際及便于分層抽樣,認定全校教師人數為
千步為超健康生活方式者,其他為一般生活方式者,學校委托數學組調查,數學組采用分層抽樣的辦法去估計全校師生的情況,結合實際及便于分層抽樣,認定全校教師人數為![]() 人,高一學生人數為
人,高一學生人數為![]() 人,高二學生人數
人,高二學生人數![]() 人,高三學生人數
人,高三學生人數![]() ,從中抽取
,從中抽取![]() 人作為調查對象,得到了如圖所示的這
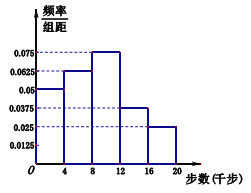
人作為調查對象,得到了如圖所示的這![]() 人的頻率分布直方圖,這
人的頻率分布直方圖,這![]() 人中有
人中有![]() 人被學校界定為不健康生活方式者.
人被學校界定為不健康生活方式者.
(1)求這次作為抽樣調查對象的教師人數;
(2)根據頻率分布直方圖估算全校師生每人一天走路步數的中位數(四舍五入精確到整數步);
(3)校辦公室欲從全校師生中速記抽取![]() 人作為“每天一萬步”活動的慰問對象,計劃學校界定不健康生活方式者鞭策性精神鼓勵
人作為“每天一萬步”活動的慰問對象,計劃學校界定不健康生活方式者鞭策性精神鼓勵![]() 元,超健康生活方式者表彰獎勵
元,超健康生活方式者表彰獎勵![]() 元,一般生活方式者鼓勵性獎勵
元,一般生活方式者鼓勵性獎勵![]() 元,利用樣本估計總體,將頻率視為概率,求這次校辦公室慰問獎勵金額恰好為
元,利用樣本估計總體,將頻率視為概率,求這次校辦公室慰問獎勵金額恰好為![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,其前n項和為Sn , {bn}是等比數列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求數列{an}與{bn}的通項公式;
(2)記Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在實數p,q,r,對于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在極坐標系(與直角坐標系
為參數),在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com