
【題目】某校對2000名高一新生進行英語特長測試選拔,現抽取部分學生的英語成績,將所得數據整理后得出頻率分布直方圖如圖所示,圖中從左到右各小長方形面積之比為![]() ,第二小組頻數為12.
,第二小組頻數為12.
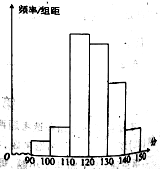
(Ⅰ)求第二小組的頻率及抽取的學生人數;
(Ⅱ)若分數在120分以上(含120分)才有資格被錄取,約有多少學生有資格被錄取?
(Ⅲ)學校打算從分數在![]() 和
和![]() 分內的學生中,按分層抽樣抽取4人進行改進意見問卷調查,若調查老師隨機從這4人的問卷中(每人一份)隨機抽取兩份調閱,求這兩份問卷都來自英語測試成績在
分內的學生中,按分層抽樣抽取4人進行改進意見問卷調查,若調查老師隨機從這4人的問卷中(每人一份)隨機抽取兩份調閱,求這兩份問卷都來自英語測試成績在![]() 分的學生的概率.
分的學生的概率.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
試題分析:(Ⅰ)頻率分布直方圖中小長方形面積等于對應區間概率,所以第二小組的頻率:![]() ,因此抽取的學生人數是
,因此抽取的學生人數是![]() 人(Ⅱ)先確定概率:有資格被錄取的學生頻率約為
人(Ⅱ)先確定概率:有資格被錄取的學生頻率約為![]() ,再確定人數
,再確定人數![]() 人(Ⅲ)先按分層抽樣確定分數在
人(Ⅲ)先按分層抽樣確定分數在![]() 和
和![]() 所抽人數比為
所抽人數比為![]() ,即4人有3人分數在
,即4人有3人分數在![]() 分內,再利用枚舉法確定隨機抽取兩份可能數為6種,而這兩份問卷都來自
分內,再利用枚舉法確定隨機抽取兩份可能數為6種,而這兩份問卷都來自![]() 有3種,因此所求概率為
有3種,因此所求概率為![]()
試題解析:(Ⅰ)∵頻率分布直方圖以面積的形式反映了數據落在各小組內的頻率大小,
∴第二小組的頻率:![]() ;
;
∵第二小組頻數為12,∴抽取的學生人數是![]() 人.
人.
(Ⅱ)由圖知,有資格被錄取的學生頻率約為![]() ,
,
∴約有![]() 人
人
(Ⅲ)由圖知,分數在![]() 分內的學生的頻率
分內的學生的頻率![]() ,
,
∵共有2000學生參加測試,∴分數在![]() 分內的學生約為
分內的學生約為![]() 人,
人,
分數在![]() 分內的學生約為
分內的學生約為![]() 人.
人.
故按分層抽樣的4人有3人分數在![]() 分內,設為
分內,設為![]() ;
;
有1人分數在![]() 分內,設為
分內,設為![]() .任取兩人,有
.任取兩人,有![]() 共6種.
共6種.
這兩人都是分數在![]() 分內的有
分內的有![]() 三種,故所求概率為
三種,故所求概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】某中學高三文科班學生參加了數學與地理水平測試,學校從測試合格的學生中隨機抽取100人的成績進行統計分析.抽取的100人的數學與地理的水平測試成績如下表:

成績分為優秀、良好、及格三個等級,橫向、縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42人.
(1)若在該樣本中,數學成績優秀率為30%,求a,b的值;
(2)若樣本中![]() ,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年1月,某國宣布成功進行氫彈試驗后,A,B,C,D四國領導人及聯合國主席紛紛表示譴責,就此,某電視臺特別邀請一軍事專家對這一事件進行評論,若該軍事專家計劃從A,B,C,D四國及聯合國主席這5個領導人中任選2人的發言態度進行評論,那么,他評論的這2人中至少包括A、B一國領導人的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐PABCD的三視圖如圖所示,四棱錐PABCD的五個頂點都在一個球面上, E,F分別是棱AB,CD的中點,直線EF被球面所截得的線段長為2![]() ,則該球的表面積為
,則該球的表面積為
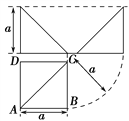
A. 12π B. 24π C. 36π D. 48π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (a為常數)有兩個極值點.
(a為常數)有兩個極值點.
(1)求實數a的取值范圍;
(2)設f(x)的兩個極值點分別為x1,x2,若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
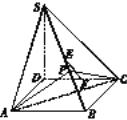
【題目】四棱錐S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分別為SB、CD的中點.
(Ⅰ)求證:EF∥平面SAD;
(Ⅱ)點P是SB上一點,若SB⊥平面APC,試確定點P的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線C:
為拋物線C:![]() 的焦點,過點
的焦點,過點![]() 的動直線
的動直線![]() 與拋物線C交于
與拋物線C交于![]() ,
,![]() 兩點,如圖.當直線
兩點,如圖.當直線![]() 與
與![]() 軸垂直時,
軸垂直時,![]() .
.
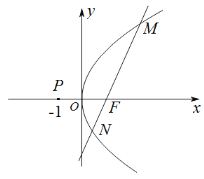
(1)求拋物線C的方程;
(2)已知點![]() ,設直線PM的斜率為
,設直線PM的斜率為![]() ,直線PN的斜率為
,直線PN的斜率為![]() .請判斷
.請判斷![]() 是否為定值,若是,寫出這個定值,并證明你的結論;若不是,說明理由.
是否為定值,若是,寫出這個定值,并證明你的結論;若不是,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com