Question

【題目】(2017全國Ⅱ,文19)海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg),其頻率分布直方圖如下:

舊養殖法

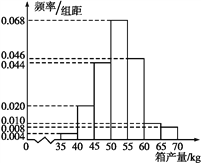
新養殖法

(1)記A表示事件“舊養殖法的箱產量低于50 kg”,估計A的概率;

(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關;

	箱產量<50 kg	箱產量≥50 kg
舊養殖法
新養殖法

(3)根據箱產量的頻率分布直方圖,對這兩種養殖方法的優劣進行比較.

附:,

Answer 1

【答案】（1）0.62（2）有（3）新養殖法優于舊養殖法.

【解析】試題分析: (1)根據頻率分布直方圖中小長方形面積等于對應概率,計算出事件A的概率;(2)將數據填入表格,代入卡方公式,計算出的數值與表哥中參考數據對照可做出判斷;(3)先從均值比較大小,再從數據分布情況看穩定性,綜上可得結論.

試題解析:

(1)舊養殖法的箱產量低于50 kg的頻率為(0.012+0.014+0.024+0.034+0.040)×5=0.62.

因此,事件A的概率估計值為0.62.

(2)根據箱產量的頻率分布直方圖得列聯表

	箱產量<50 kg	箱產量≥50 kg
舊養殖法	62	38
新養殖法	34	66

K2=≈15.705.

由于15.705>6.635,故有99%的把握認為箱產量與養殖方法有關.

(3)箱產量的頻率分布直方圖表明:新養殖法的箱產量平均值(或中位數)在50 kg到55 kg之間,舊養殖法的箱產量平均值(或中位數)在45 kg到50 kg之間,且新養殖法的箱產量分布集中程度較舊養殖法的箱產量分布集中程度高,因此,可以認為新養殖法的箱產量較高且穩定,從而新養殖法優于舊養殖法.

點睛:(1)頻率分布直方圖中小長方形的面積等于對應的概率,所以小長方形的面積之和為1;(2)頻率分布直方圖中均值等于組中值域對應概率乘積之和;(3)均值大小代表水平高低,均值越大水平越高,方差大小代表穩定性,方差或標準差的值越小,代表越穩定,且集中程度高.