
【題目】已知![]() 元集合
元集合![]() 的一些子集滿足:每個子集至少含2個元素,每兩個不同子集的交集至多含2個元素,記這些子集的元素個數(shù)的立方和為
的一些子集滿足:每個子集至少含2個元素,每兩個不同子集的交集至多含2個元素,記這些子集的元素個數(shù)的立方和為![]() .問:是否存在不小于3的正整數(shù)
.問:是否存在不小于3的正整數(shù)![]() ,使
,使![]() 的最大值等于2009的方冪?說明你的理由.
的最大值等于2009的方冪?說明你的理由.
【答案】見解析
【解析】
設![]() 取最大值時,對應有
取最大值時,對應有![]() 個子集
個子集![]() .則
.則![]() .
.
若存在某個![]() ,使
,使![]() ,不妨設為
,不妨設為![]() ,將
,將![]() 的所有三元子集記為
的所有三元子集記為![]() ,則
,則![]() .
.
對任意的![]() ,有
,有![]() .
.
對任意的![]() ,有
,有![]() .
.
由已知,對任意的![]() ,
,![]() ,有
,有
![]() .
.
故可用![]() 替換原先的
替換原先的![]() ,形成新的子集族.
,形成新的子集族.
因![]()
![]() ,
,
所以,替換后所有集合元素個數(shù)的立方和增加,這與![]() 的最大性矛盾.
的最大性矛盾.
于是,當![]() 取最大值時,每個子集元素的個數(shù)都不大于3.
取最大值時,每個子集元素的個數(shù)都不大于3.
又取一切![]() 的二元子集和三元子集形成的子集族滿足題意,于是,它們的元素個數(shù)的立方和為
的二元子集和三元子集形成的子集族滿足題意,于是,它們的元素個數(shù)的立方和為![]()
![]()
![]() .
.
假設![]() .則
.則
![]() . ①
. ①
若![]() 是偶數(shù),則
是偶數(shù),則![]() 是偶數(shù).從而,式①左邊是4的倍數(shù),矛盾.
是偶數(shù).從而,式①左邊是4的倍數(shù),矛盾.
所以,![]() 是奇數(shù).
是奇數(shù).
記![]() ,則
,則
![]() 是10的約數(shù).
是10的約數(shù).
結(jié)合式①知![]() .
.
又因![]() ,
,![]() ,所以,當
,所以,當![]() 時,式①左邊的三個因數(shù)的質(zhì)因子互不相同,故只可能
時,式①左邊的三個因數(shù)的質(zhì)因子互不相同,故只可能![]() .此時,
.此時,![]() ,而式①右邊不含質(zhì)因子3,矛盾.
,而式①右邊不含質(zhì)因子3,矛盾.
綜上,不存在不小于3的正整數(shù)![]() ,使
,使![]() 的最大值等于2009的方冪.
的最大值等于2009的方冪.


科目:高中數(shù)學 來源: 題型:
【題目】十九大指出,必須樹立“綠水青山就是金山銀山”的生態(tài)文明發(fā)展理念,這一理念將進一步推動新能源汽車產(chǎn)業(yè)的迅速發(fā)展![]() 以下是近幾年我國新能源汽車的年銷量數(shù)據(jù)及其散點圖
以下是近幾年我國新能源汽車的年銷量數(shù)據(jù)及其散點圖![]() 如圖所示
如圖所示![]() :
:
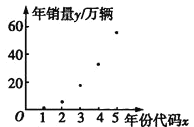
年份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
新能源汽車的年銷量 |
|
|
|
|
|
(1)請根據(jù)散點圖判斷![]() 與
與![]() 中哪個更適宜作為新能源汽車年銷量
中哪個更適宜作為新能源汽車年銷量![]() 關于年份代碼
關于年份代碼![]() 的回歸方程模型?
的回歸方程模型?![]() 給出判斷即可,不必說明理由)
給出判斷即可,不必說明理由)
(2)根據(jù)![]() 的判斷結(jié)果及表中數(shù)據(jù),建立
的判斷結(jié)果及表中數(shù)據(jù),建立![]() 關于
關于![]() 的回歸方程,并預測2019年我國新能源汽車的年銷量
的回歸方程,并預測2019年我國新能源汽車的年銷量![]() 精確到
精確到![]()
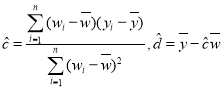
附令![]() ,
,
|
|
|
|
|
| 10 | 374 |
| 851.2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中學的環(huán)保社團參照國家環(huán)境標準制定了該校所在區(qū)域空氣質(zhì)量指數(shù)與空氣質(zhì)量等級對應關系如下表(假設該區(qū)域空氣質(zhì)量指數(shù)不會超過300):
空氣質(zhì)量指數(shù) |
|
|
|
|
|
|
空氣質(zhì)量等級 | 1級優(yōu) | 2級良 | 3級輕度污染 | 4級中度污染 | 5級重度污染 | 6級嚴重污染 |
該社團將該校區(qū)在2018年100天的空氣質(zhì)量指數(shù)監(jiān)測數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如圖,把該直方圖所得頻率估計為概率.

(1)請估算2019年(以365天計算)全年該區(qū)域空氣質(zhì)量優(yōu)良的天數(shù)(未滿一天按一天計算);
(2)該校2019年6月7、8日將作為高考考場,若這兩天中某天出現(xiàn)5級重度污染,需要凈化空氣費用8000元,出現(xiàn)6級嚴重污染,需要凈化空氣費用12000元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”,三國時期吳國的數(shù)學家趙爽在《周髀算經(jīng)》中注釋了其理論證明,其基本思想是圖形經(jīng)過割補后面積不變.即通過如圖所示的“弦圖”,將勻股定理表述為:“勾股各自乘,并之,為弦實,開方除之,即弦”(其中![]() 分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即
分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即![]() ,化簡得
,化簡得![]() .現(xiàn)已知
.現(xiàn)已知![]() ,
,![]() ,向外圍大正方形
,向外圍大正方形![]() 區(qū)域內(nèi)隨機地投擲一枚飛鏢,飛鏢落在中間小正方形
區(qū)域內(nèi)隨機地投擲一枚飛鏢,飛鏢落在中間小正方形![]() 內(nèi)的概率是( )
內(nèi)的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地有A,B、C、D四人先后感染了新型冠狀病毒,其中只有A到過疫區(qū),B肯定是受A感染的,對于C,因為難以判定他是受A還是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同樣也假設D受A、B和C感染的概率都是
,同樣也假設D受A、B和C感染的概率都是![]() .在這種假定之下,B、C、D中直接受A感染的人數(shù)X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數(shù)學期望)為______.
.在這種假定之下,B、C、D中直接受A感染的人數(shù)X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數(shù)學期望)為______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
,![]() )的圖像經(jīng)過點
)的圖像經(jīng)過點![]() ,且關于直線
,且關于直線![]() 對稱,則下列結(jié)論正確的是( )
對稱,則下列結(jié)論正確的是( )
A. ![]() 在
在![]() 上是減函數(shù)
上是減函數(shù)
B. 函數(shù)的最小正周期為![]()
C. ![]() 的解集是
的解集是![]() ,
,![]()
D. ![]() 的一個對稱中心是
的一個對稱中心是![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 的頂點在坐標原點,其焦點
的頂點在坐標原點,其焦點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 為直線
為直線![]() 上一點,圓
上一點,圓![]() 與
與![]() 軸相切(
軸相切(![]() 為圓心),且
為圓心),且![]() ,
,![]() 關于點
關于點![]() 對稱.
對稱.
(1)求圓![]() 和拋物線
和拋物線![]() 的標準方程;
的標準方程;
(2)過![]() 的直線
的直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,交拋物線
兩點,交拋物線![]() 于
于![]() ,
,![]() 兩點,求證:
兩點,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】過直線![]() 上的點
上的點![]() 作橢圓
作橢圓![]() 的切線
的切線![]() ,切點分別為
,切點分別為![]() ,聯(lián)結(jié)
,聯(lián)結(jié)![]() .
.
(1)當點![]() 在直線
在直線![]() 上運動時,證明:直線
上運動時,證明:直線![]() 恒過定點
恒過定點![]() ;
;
(2)當![]() 時,定點
時,定點![]() 平分線段
平分線段![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com